<- previous index next ->
Hopefully you understand decimal division:
49 quotient
______
divisor 47 / 2345 dividend
188
---
465
423
---
42 remainder
And check division by multiplication:
49 multiplicand is the quotient above
x 47 multiplier is the divisor above
----
2303
+ 42 add the remainder above
----
2345 final sum is the dividend above
A smaller case that is used below in binary:
12 quotient
___
divisor 7 / 85 dividend
7
--
15
14
--
1 remainder
Binary divide, conventional method and non restoring method
These examples are shown in a form that can be directly
implemented in a computer architecture.
The divisor, quotient and remainder are each one word.
The dividend is two words.
The equations dividend = quotient * divisor + remainder
and |remainder| < |divisor|
must be satisfied.
When a choice is possible, choose the sign of the remainder to
be the same as the sign of the dividend.
Save the sign bits of the dividend and divisor, if necessary,
negate the dividend and divisor to make them positive.
Fix up the sign bits of the quotient and dividend after dividing.
Example: dividend = 85 , divisor = 7
Decimal divide 85 / 7 = quotient 12 , remainder 1
Restoring (conventional) binary divide, twos complement 4-bit numbers
1 1 0 0 quotient
________________
0 1 1 1 / 0 1 0 1 0 1 0 1
-0 1 1 1 may subtract by adding twos complement
_______ - 0 1 1 1 is 1 0 0 1
5 - 7 = -2 1 1 1 0
negative, add 7 +0 1 1 1
restored _______
next bit 1 0 1 0
-0 1 1 1
_______
10 - 7 = 3 0 1 1 1
quotient=1, next bit -0 1 1 1
_______
7 - 7 = 0 0 0 0 0 0
quotient=1, next bit -0 1 1 1
_______
0 - 7 = -7 1 0 0 1
negative, add 7 +0 1 1 1
quotient=0 _______
restored, next bit 0 0 0 1
-0 1 1 1
_______
1 - 7 = -6 1 0 1 0
negative, add 7 +0 1 1 1
quotient=0 _______
restored, finished 0 0 0 1 final remainder
(8 cycles using adder)
Clock cycles can be saved by not performing the "restored" operation.
non-restoring binary divide, twos complement 4-bit numbers
note: 7 = 0 1 1 1 -7 = 1 0 0 1
1 1 0 0 quotient
________________
0 1 1 1 / 0 1 0 1 0 1 0 1
pre shift +1 0 0 1 adding twos complement of divisor
_______
10 - 7 = 3 0 0 1 1 1
quotient=1 +1 0 0 1
next bit subtract _______
7 - 7 = 0 0 0 0 0 0
quotient=1 +1 0 0 1
next bit subtract _______
0 - 7 = -7 1 0 0 1 1
quotient=0 +0 1 1 1 adding divisor
next bit add _______
2 + 7 = 9 = -7 1 0 1 0
quotient=0 +0 1 1 1
correction add _______
final remainder 0 0 0 1 remainder
(5 cycles using adder)
Correcting signs:
dividend divisor | quotient remainder
------------------+--------------------
+ + | + + +85 / +7 = +12 R +1
+ - | - + +85 / -7 = -12 R +1
- + | - - -85 / +7 = -12 R -1
- - | + - -85 / -7 = +12 R -1
Humans, not the computer, keeps track of the binary point.
Integers Fractions (fixed point)
qqqq. .qqqq q.qqq
__________ __________ __________
ssss. / dddddddd. .ssss / .dddddddd ss.ss / ddd.ddddd
_____ _____ _______
rrrr. .0000rrrr .0rrrr
qqqq. .qqqq q.qqq
* ssss. * .ssss * ss.ss
_________ ________ _________
tttttttt. .tttttttt ttt.ttttt
+ rrrr. + .0000rrrr + .0rrrr
_________ _________ _________
dddddddd. .dddddddd ddd.ddddd
for multiply, counting positions from the right, the binary point
of the product is at the sum of the positions of the multiplicand
and multiplier.
for divide, counting positions from the right, the binary point
of the quotient is at the difference of the positions of the
dividend and divisor. The binary point of the remainder is in
the same position as the binary point of the dividend.
Overflow occurs when the top half of dividend is greater than or
equal to the divisor, thus division by zero is always overflow.
No schematic or VHDL is provided for restoring division because
it is never used in practice. The serial non restoring division is:
A possible design for a serial divide, does not include remainder correction:
diva <= hi(30 downto 0) & lo(31) after 50 ps; -- shift
divb <= not md when sub_add='1' else md after 50 ps; -- subtract or add
adder:entity WORK.add32 port map(diva, divb, sub_add, divs, cout);
quo <= not divs(31) after 50 ps; -- quotient bit
hi <= divs when divclk'event and divclk='1';
lo <= lo(30 downto 0) & quo when divclk'event and divclk='1';
sub_add <= quo when divclk'event and divclk='1';
 The full VHDL code is div_ser.vhdl
with output div_ser.out
Note that the remainder is not corrected by this circuit.
The FFFFFFFA should have the divisor 00000007 added to it,
making the remainder 00000001
Now that you understand how binary division works and understand
how multiplication can be speeded up using parallel circuits,
we show a parallel division circuit and its simulation.
The full VHDL code is div_ser.vhdl
with output div_ser.out
Note that the remainder is not corrected by this circuit.
The FFFFFFFA should have the divisor 00000007 added to it,
making the remainder 00000001
Now that you understand how binary division works and understand
how multiplication can be speeded up using parallel circuits,
we show a parallel division circuit and its simulation.
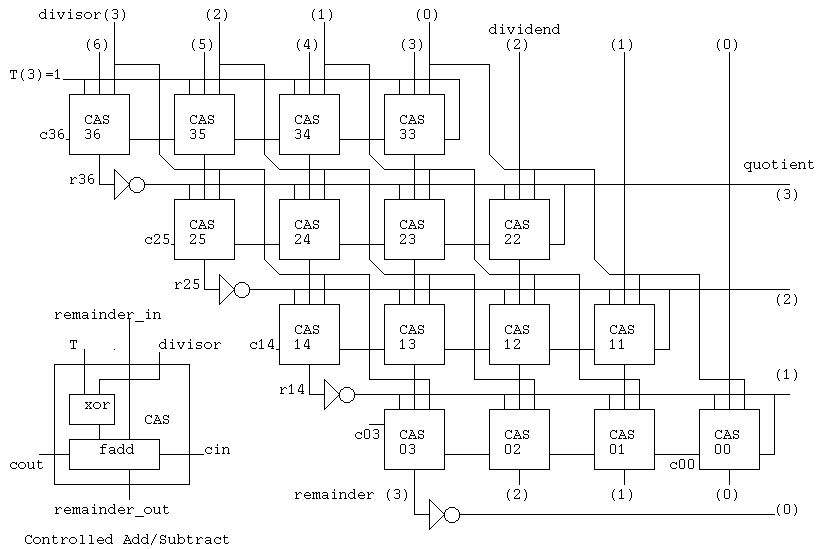 divcas4_test.vhdl
divcas4_test.out
Note that the output includes the time.
Observe the first few lines of printout replacing 'U' undefined,
meaning not computed, with zeros or ones. Unfortunately, if VHDL
prints hexadecimal, any state except one is printed as zero.
For part1 project you are given divcas16.vhdl
This divides as 32 bit number by a 16 bit number and
produces a 16 bit quotient and 16 bit remainder.
divcas16.vhdl
It would be nice if I could have a 4-bit radix 2 or radix 4 SRT
division schematic here. Parallel circuits that perform division
may use (-2, -1, 0, 1, 2) values for intermediate signals.
Two or more bits of the quotient may be computed at each stage,
based on a table and a few bits of the divisor and partial
remainder.
SRT Divide, click on slide show .pdf
SRT Divide .pdf local
freepatentsonline.com/5272660.html
Software can be copyrighted. Just doing a physical embodiment makes
you the owner of the copyright. Add Copyright year name to the
document or computer file. If you want your copyright to stand up
in a court of law, you need to file the copyright. Get the latest
information, at one time there was a $40.00 filing fee and the
copyright was good for 28 years, renewable for 67 more years, for
a total of 95 years.
There is a "fair use" clause that allows personal use of parts
of a copyrighted document.
Software and hardware and processes may be patented. A utility
patent is good for 20 years, a design patent is good for 14 years.
The cost of completing the process of getting a patent is variable.
20 years ago the average cost was $5,000.00 and today the average
cost is about $15,000.00. There are companies that can help you,
do-it-yourself, with advertised cost starting from about $1,500.00.
(There may be additional maintenance fees at 3 1/2 years etc.)
((It may take a year or more to get a patent.))
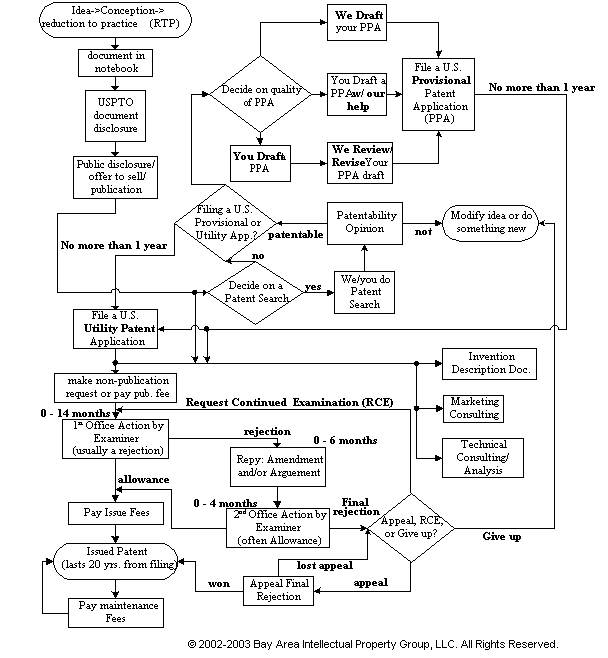
One version of the process to get a patent is:
divcas4_test.vhdl
divcas4_test.out
Note that the output includes the time.
Observe the first few lines of printout replacing 'U' undefined,
meaning not computed, with zeros or ones. Unfortunately, if VHDL
prints hexadecimal, any state except one is printed as zero.
For part1 project you are given divcas16.vhdl
This divides as 32 bit number by a 16 bit number and
produces a 16 bit quotient and 16 bit remainder.
divcas16.vhdl
It would be nice if I could have a 4-bit radix 2 or radix 4 SRT
division schematic here. Parallel circuits that perform division
may use (-2, -1, 0, 1, 2) values for intermediate signals.
Two or more bits of the quotient may be computed at each stage,
based on a table and a few bits of the divisor and partial
remainder.
SRT Divide, click on slide show .pdf
SRT Divide .pdf local
freepatentsonline.com/5272660.html
Software can be copyrighted. Just doing a physical embodiment makes
you the owner of the copyright. Add Copyright year name to the
document or computer file. If you want your copyright to stand up
in a court of law, you need to file the copyright. Get the latest
information, at one time there was a $40.00 filing fee and the
copyright was good for 28 years, renewable for 67 more years, for
a total of 95 years.
There is a "fair use" clause that allows personal use of parts
of a copyrighted document.
Software and hardware and processes may be patented. A utility
patent is good for 20 years, a design patent is good for 14 years.
The cost of completing the process of getting a patent is variable.
20 years ago the average cost was $5,000.00 and today the average
cost is about $15,000.00. There are companies that can help you,
do-it-yourself, with advertised cost starting from about $1,500.00.
(There may be additional maintenance fees at 3 1/2 years etc.)
((It may take a year or more to get a patent.))
One version of the process to get a patent is:
 There is no "fair use" clause on patents.
There is no "fair use" clause on patents.
<- previous index next ->
 The full VHDL code is div_ser.vhdl
with output div_ser.out
Note that the remainder is not corrected by this circuit.
The FFFFFFFA should have the divisor 00000007 added to it,
making the remainder 00000001
Now that you understand how binary division works and understand
how multiplication can be speeded up using parallel circuits,
we show a parallel division circuit and its simulation.
The full VHDL code is div_ser.vhdl
with output div_ser.out
Note that the remainder is not corrected by this circuit.
The FFFFFFFA should have the divisor 00000007 added to it,
making the remainder 00000001
Now that you understand how binary division works and understand
how multiplication can be speeded up using parallel circuits,
we show a parallel division circuit and its simulation.
 divcas4_test.vhdl
divcas4_test.out
Note that the output includes the time.
Observe the first few lines of printout replacing 'U' undefined,
meaning not computed, with zeros or ones. Unfortunately, if VHDL
prints hexadecimal, any state except one is printed as zero.
For part1 project you are given divcas16.vhdl
This divides as 32 bit number by a 16 bit number and
produces a 16 bit quotient and 16 bit remainder.
divcas16.vhdl
It would be nice if I could have a 4-bit radix 2 or radix 4 SRT
division schematic here. Parallel circuits that perform division
may use (-2, -1, 0, 1, 2) values for intermediate signals.
Two or more bits of the quotient may be computed at each stage,
based on a table and a few bits of the divisor and partial
remainder.
SRT Divide, click on slide show .pdf
SRT Divide .pdf local
freepatentsonline.com/5272660.html
Software can be copyrighted. Just doing a physical embodiment makes
you the owner of the copyright. Add Copyright year name to the
document or computer file. If you want your copyright to stand up
in a court of law, you need to file the copyright. Get the latest
information, at one time there was a $40.00 filing fee and the
copyright was good for 28 years, renewable for 67 more years, for
a total of 95 years.
There is a "fair use" clause that allows personal use of parts
of a copyrighted document.
Software and hardware and processes may be patented. A utility
patent is good for 20 years, a design patent is good for 14 years.
The cost of completing the process of getting a patent is variable.
20 years ago the average cost was $5,000.00 and today the average
cost is about $15,000.00. There are companies that can help you,
do-it-yourself, with advertised cost starting from about $1,500.00.
(There may be additional maintenance fees at 3 1/2 years etc.)
((It may take a year or more to get a patent.))
One version of the process to get a patent is:
divcas4_test.vhdl
divcas4_test.out
Note that the output includes the time.
Observe the first few lines of printout replacing 'U' undefined,
meaning not computed, with zeros or ones. Unfortunately, if VHDL
prints hexadecimal, any state except one is printed as zero.
For part1 project you are given divcas16.vhdl
This divides as 32 bit number by a 16 bit number and
produces a 16 bit quotient and 16 bit remainder.
divcas16.vhdl
It would be nice if I could have a 4-bit radix 2 or radix 4 SRT
division schematic here. Parallel circuits that perform division
may use (-2, -1, 0, 1, 2) values for intermediate signals.
Two or more bits of the quotient may be computed at each stage,
based on a table and a few bits of the divisor and partial
remainder.
SRT Divide, click on slide show .pdf
SRT Divide .pdf local
freepatentsonline.com/5272660.html
Software can be copyrighted. Just doing a physical embodiment makes
you the owner of the copyright. Add Copyright year name to the
document or computer file. If you want your copyright to stand up
in a court of law, you need to file the copyright. Get the latest
information, at one time there was a $40.00 filing fee and the
copyright was good for 28 years, renewable for 67 more years, for
a total of 95 years.
There is a "fair use" clause that allows personal use of parts
of a copyrighted document.
Software and hardware and processes may be patented. A utility
patent is good for 20 years, a design patent is good for 14 years.
The cost of completing the process of getting a patent is variable.
20 years ago the average cost was $5,000.00 and today the average
cost is about $15,000.00. There are companies that can help you,
do-it-yourself, with advertised cost starting from about $1,500.00.
(There may be additional maintenance fees at 3 1/2 years etc.)
((It may take a year or more to get a patent.))
One version of the process to get a patent is:
 There is no "fair use" clause on patents.
There is no "fair use" clause on patents.