<- previous index next ->
Example of a Deterministic Finite Automata, DFA
Machine Definition M = (Q, Sigma, delta, q0, F)
Q = { q0, q1, q2, q3, q4 } the set of states (finite)
Sigma = { 0, 1 } the input string alphabet (finite)
delta the state transition table - below
q0 = q0 the starting state
F = { q2, q4 } the set of final states (accepting
when in this state and no more input)
inputs
delta | 0 | 1 |
---------+---------+---------+
q0 | q3 | q1 |
q1 | q1 | q2 |
states q2 | q2 | q2 |
q3 | q4 | q3 |
q4 | q4 | q4 |
^ ^ ^
| | |
| +---------+-- every transition must have a state
+-- every state must be listed
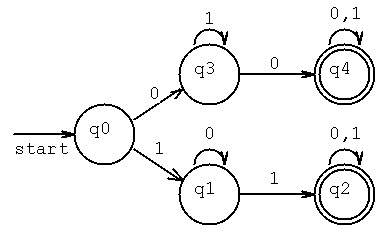
An exactly equivalent diagram description for the machine M.
Each circle is a unique state. The machine is in exactly one state
and stays in that state until an input arrives. Connection lines
with arrows represent a state transition from the present state
to the next state for the input symbol(s) by the line.
L(M) is the notation for a Formal Language defined by a machine M.
Some of the shortest strings in L(M) = { 00, 11, 000, 001, 010, 101, 110,
111, 0000, 0001, 0010, 0011, 0100, 0101, 0110, 1001, ... }
The regular expression for this state diagram is
r = (0(1*)0(0+1)*)+(1(0*)1(0+1)*) using + for or, * for kleene star
1|--|
| V
//--\\
|| q3 || is a DFA with regular expression r = (1*)
\\--// zero or more sequence of 1 (infinite language)
0|--|
1| v
//--\\ is a DFA with regular expression r = (0+1)*
|| q4 || zero or more sequence of 0 or 1 in any order 00 01 10 11 etc
\\--// at end because final state (infinite language)
In words, L is the set of strings over { 0, 1} that contain at least
two 0's starting with 0, or that contain at least two 1's starting with 1.
Every input sequence goes through a sequence of states, for example
00 q0 q3 q4
11 q0 q1 q2
000 q0 q3 q4 q4
001 q0 q3 q4 q4
010 q0 q3 q3 q4
011 q0 q3 q3 q3
0110 q0 q3 q3 q3 q4
Rather abstract, there are tens of millions of DFA being used today.
practical example DFA
More information on DFA
More files, examples:
example data input file reg.dfa
example output from dfa.cpp, reg.out
under development dfa.java dfa.py
example output from dfa.java, reg_def_java.out
example output from dfa.py, labc_def_py.out
/--\ a /--\ b /--\ c //--\\
labc.dfa is -->| q0 |--->| q1 |--->| q2 |--->|| q3 || using just characters
\--/ \--/ \--/ \\--//
example data input file labc.dfa
example output from dfa.py, labc_def_py.out
For future homework, you can download programs and sample data from
cp /afs/umbc.edu/users/s/q/squire/pub/download/reg.dfa .
and other files
Definition of a Regular Expression
------------------
A regular expression may be the null string,
r = epsilon
A regular expression may be an element of the input alphabet, a in sigma,
r = a
A regular expression may be the union of two regular expressions,
r = r1 + r2 the plus sign is "or"
A regular expression may be the concatenation (no symbol) of two
regular expressions,
r = r1 r2
A regular expression may be the Kleene closure (star) of a
regular expression, may be null string or any number of concatenations of r1
r = r1* (the asterisk should be a superscript,
but this is plain text)
A regular expression may be a regular expression in parenthesis
r = (r1)
Nothing is a regular expression unless it is constructed with only the
rules given above.
The language represented or generated by a regular expression is a
Regular Language, denoted L(r).
The regular expression for the machine M above is
r = (1(0*)1(0+1)*)+(0(1*)0(0+1)*)
\ \ any number of zeros and ones
\ any number of zero
Later we will give an algorithm for generating a regular expression from
a machine definition. For simple DFA's, start with each accepting
state and work back to the start state writing the regular expression.
The union of these regular expressions is the regular expression for
the machine.
For every DFA there is a regular language and for every regular language
there is a regular expression. Thus a DFA can be converted to a
regular expression and a regular expression can be converted to a DFA.
Some examples, a regular language with only 0 in alphabet,
with strings of length 2*n+1 for n>0. Thus infinite language yet
DFA must have a finite number of states and finite number of
transitions to accept {000, 00000, 0000000, ...) 2*n+1 = 3,5,7,...
The DFA state diagram is
/--\ 0 /--\ 0 /--\ 0 //--\\ 0
| q0 |-->| q0 |-->| q0 |--->|| q4 ||--+
\--/ \--/ \--/ \\--// |
^ |
+---------------+
Check it out: 000 accepted, then 00000 two more 0 then accepted, ...
Now, an example of the complement of a regular expression is
a regular expression. First a DFA that accepts any string with 00
then a DFA that does not accept any string with 00, the complement.
|--|<-------+ |--------+ r = ((1)*0)*0(0+1)*
V |1 |1 V |
/--\ 0 /--\ 0 //--\\ |1 any 00
-| q0 |-->| q1 |-->|| q2 ||--+ (1)* can be empty string
\--/ \--/ \\--// |0
^ |
|--------+
+-----------------+
| /--\-+ 1 /--\ 0
| +-->| q1 |--->| q2 |----+ r = ((1*)+0(1*))*
V 0 | \--/ 0 \--/---+ |
//--\\---+ ^ ^ 1| | no 00
-|| q0 || | +---+ |
\\--//---+ +--------+
^ 1 | never leaves, never accepted
+----+
The general way to create a complement of a regular expression is to
create a new regular expression that has all of the first regular
expression go to phi and all other strings go to a final state.
Both regular expressions must have the same alphabet.
Given a DFA and one or more strings, determine if the string(s)
are accepted by the DFA. This may be error prone and time
consuming to do by hand. Fortunately, there is a program
available to do this for you.
On linux.gl.umbc.edu do the following:
ln -s /afs/umbc.edu/users/s/q/squire/pub/dfa dfa
cp /afs/umbc.edu/users/s/q/squire/pub/download/ab_b.dfa .
dfa < ab_b.dfa # or dfa < ab_b.dfa > ab_a.out
Full information is available at Simulators
The source code for the family of simulators is available.
HW2 is assigned
last update 3/9/2021
<- previous index next ->

