Before clipping
| 5.Clipping |
![[prev]](common/prev.gif)
![[next]](common/next.gif)
|
Before clipping |
|
After clipping |
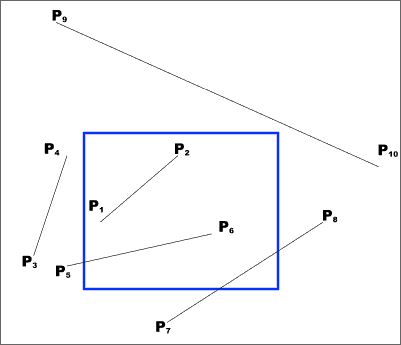
Point Clipping
|
Point Clipping
Line ClippingIf both points lie inside the window
|
Point Clipping
Line ClippingIf both points lie inside the window
If both points lie outside the same boundary
|
Point Clipping
If both points lie inside the window
If both points lie outside the same boundary
If segment crosses one or more boundaries
|
Cohen - Sutherland Line Clipping
|
Cohen - Sutherland Line Clipping
|
Cohen - Sutherland Line Clipping
|
Cohen - Sutherland Line Clipping
|
Cohen - Sutherland Line Clipping
|
Cohen - Sutherland Line Clipping
|
|||||||||||||
Cohen - Sutherland Line Clipping
|
|||||||||||||||||
Cohen - Sutherland Line Clipping
|
|||||||||||||||||||||||
Cohen - Sutherland Line Clipping
|
|||||||||||||||||||||||||||||
Cohen - Sutherland Line Clipping
|
|||||||||||||||||||||||||||||||||||
Cohen - Sutherland Line Clipping: Algorithm
For each line segment
(1) compute clip codes
(2) if both are 0 0 0 0
accept line segment
else if c1 & c2 != 0
discard line segment
else /* c1 & c2 = 0 */
clip against left
clip against right
clip against bottom
clip against top
if anything remains
accept clipped segment
|
Cohen - Sutherland: Multiple Intersections
|
Cohen - Sutherland: Multiple Intersections
|
Cohen - Sutherland: Multiple Intersections
|
Cohen - Sutherland: Multiple Intersections
|
Parametric Line Clipping (Cyrus - Beck)
|
Parametric Line Clipping (Cyrus - Beck)
|
Parametric Line Clipping (Cyrus - Beck)
Compute t for each clip rectangle edge Discard values of t outside [0, 1] Classify other candidates more carefully (tL)
|
Parametric Line Clipping (Cyrus - Beck) |
Cyrus - Beck: Classifying Intersections
|
Cyrus - Beck: Classifying Intersections
Potentially entering Intersection (PE) Ni . D < 0 (angle > 90o) => tL Potentially leaving Intersection (PL) Ni . D > 0 (angle < 90o) => tT |
Cyrus - Beck: Classifying Intersections
Potentially entering Intersection (PE) Ni D < 0 (angle > 90o) => tL Potentially leaving Intersection (PL) Ni D > 0 (angle < 90o) => tT |
Cyrus - Beck: Classifying Intersections
Potentially entering Intersection (PE)
Ni D < 0 (angle > 90o) => tL
Potentially leaving Intersection (PL)
Ni D > 0 (angle < 90o) => tr
Clipped Segment Defined by:
[PEmax, PLmin]
where PEmax = MAX ( 0, all PEs )
PLmin = MIN ( 1, all PLs )
if PLmin < PEmax reject line
|
Cyrus - Beck Line Clipping: Algorithm
Recalculate Ni and select a PEi for each edge
for ( each line segment to be clipped) {
if ( P1 == P0 )
line is degenerate so clip as a point;
else {
tE = 0;
tL = 1;
for ( each candidate intersection with a clip edge ) {
if ( Ni .D != 0 ) { /* ignore edges parallel to line */
calculate t;
use sign of Ni . D to categorize as PE or PL;
if ( PE ) tE = max ( tE , t );
if ( PL ) tL = min ( tL , t );
}
}
if ( tE > tL )
return null;
else
return P(tE) and P(tL) as true clip intersections;
}
}
|
Polygon Clipping
|
Polygon Clipping
|
Polygon Clipping
|
Polygon Clipping
|
Polygon Clipping
|
Sutherland - Hodgeman: Polygon Clipping
Original polygon |
Sutherland - Hodgeman: Polygon Clipping
Clip Left |
Sutherland - Hodgeman: Polygon Clipping
Clip Right |
Sutherland - Hodgeman: Polygon Clipping
Clip Bottom |
Sutherland - Hodgeman: Polygon Clipping
Clip Top |
Sutherland - Hodgeman Polygon Clipping: Algorithm |
Sutherland - Hodgeman Polygon Clipping: Algorithm
|
Sutherland - Hodgeman Polygon Clipping: Algorithm
|
Sutherland - Hodgeman Polygon Clipping: Algorithm
|
Sutherland - Hodgeman Polygon Clipping: Algorithm
|
Sutherland - Hodgeman Polygon Clipping: Algorithm
|
Sutherland - Hodgeman : An Example
in -> P1 P2 P3 P4 |
Sutherland - Hodgeman : An Example
in -> [clip left] -> P1 - in to in -> P1 P2 P3 P4 |
Sutherland - Hodgeman : An Example
in -> [clip left] -> P1 - in to in --> P1 P2 - in to out -> P'2 P3 P4 |
Sutherland - Hodgeman : An Example
in -> [clip left] -> P1 - in to in --> P1 P2 - in to out -> P'2 P3 - out to out -> x P4 |
Sutherland - Hodgeman : An Example
in -> [clip left] ->
P1 - in to in --> P1
P2 - in to out -> P'2
P3 - out to out -> x
P4 - out to in -> P'4
-> P4
|
Sutherland - Hodgeman : An Example
in -> [clip left] -> [clip right] ->
P1 - in to in --> P1 - in to in --> P1
P2 - in to out -> P'2 - in to in --> P'2
P3 - out to out -> x
P4 - out to in -> P'4 - in to in --> P'4
-> P4 - in to in --> P4
|
Sutherland - Hodgeman : An Example
in -> [clip left] -> [clip right] -> [clip bottom] ->
P1 - in to in --> P1 - in to in --> P1 - in to in --> P1
P2 - in to out -> P'2 - in to in --> P'2
P3 - out to out -> x
P4 - out to in -> P'4 - in to in --> P'4
-> P4 - in to in --> P4
|
Sutherland - Hodgeman : An Example
in -> [clip left] -> [clip right] -> [clip bottom] ->
P1 - in to in --> P1 - in to in --> P1 - in to in --> P1
P2 - in to out -> P'2 - in to in --> P'2 - in to out -> P''2
P3 - out to out -> x
P4 - out to in -> P'4 - in to in --> P'4
-> P4 - in to in --> P4
|
Sutherland - Hodgeman : An Example
in -> [clip left] -> [clip right] -> [clip bottom] ->
P1 - in to in --> P1 - in to in --> P1 - in to in --> P1
P2 - in to out -> P'2 - in to in --> P'2 - in to out -> P''2
P3 - out to out -> x
P4 - out to in -> P'4 - in to in --> P'4 - out to in -> P''4
-> P'4
-> P4 - in to in --> P4
|
Sutherland - Hodgeman : An Example
in -> [clip left] -> [clip right] -> [clip bottom] ->
P1 - in to in --> P1 - in to in --> P1 - in to in --> P1
P2 - in to out -> P'2 - in to in --> P'2 - in to out -> P''2
P3 - out to out -> x
P4 - out to in -> P'4 - in to in --> P'4 - out to in -> P''4
-> P'4
-> P4 - in to in --> P4 - in to in --> P4
|
Sutherland - Hodgeman : An Example
in -> [clip left] -> [clip right] -> [clip bottom] -> [clip top] -> out
P1 - in to in --> P1 - in to in --> P1 - in to in --> P1 - in to in --> P1
P2 - in to out -> P'2 - in to in --> P'2 - in to out -> P''2 - in to in --> P''2
P3 - out to out -> x
P4 - out to in -> P'4 - in to in --> P'4 - out to in -> P''4 - in to in --> P''4
-> P'4 - in to in --> P'4
-> P4 - in to in --> P4 - in to in --> P4 - in to in --> P4
|
![[prev]](common/prev.gif)
![[next]](common/next.gif)
| Made by dynaPage 0.2 |