The purpose of this assignment it to make sure you can use, and give you some familiarity with two architecture analysis tools, vhdl and valgrind
Question 1: VHDL
Set up VHDL according to the UMBC VHDL guide. For use on GL, I also created an alternative template to the cs411.tar one, which you can find in ~olano/vhdl_template. This one should work for either bash or tcsh shells if you run "source vhdl_init", and avoids assumptions about where you put the files in your GL directory. To run elsewhere, see the VHDL guide for information on the open-source ghdl.
Consider this 4-bit ripple carry ALU supporting both add and subtract.
Built from this 1-bit ALU
Create a VHDL test bench for a 4-bit ALU entity. Test both add and subtract including cases that carry between bits and cases that do not. Use it to test each of the cases below:
- Create a behavioral model for the 4-bit ALU. Assume a 750 ps delay for the result.
- Create a behavioral model for the 1-bit ALU and use it to build a structural model of the 4-bit ALU. Assume a 150 ps delay for the result and 200 ps delay for the carry out.
- Create behavioral models for a two-input AND, a two-input XOR, a three-input XOR, and a 3-input OR and use them to build a structural model of the 1-bit ALU. Assume a 50 ps delay for 2-input gates and 100 ps delay for 3-input gates.
Submit your VHDL source file and test bench output for each case.
Question 2: Valgrind
Valgrind is installed on the GL servers, or you can download and install a copy on your own computer. You should write a program to find the largest eigenvalue of an NxN real symmetric matrix using the power iteration algorithm, then analyze the cache and branch prediction using valgrind.
The program
Given matrix M, a unit eigenvector v and its eigenvalue λ are defined by
![]()
Initialize the matrix M with random values between 0 and 1. Since M should be symmetric, you only need to fill in half, using M[x][y] = M[y][x] to fill in the other half.
For the power iteration algorithm to find the largest eigenvalue and its eigenvector, you first initialize a vector, b, with random values. For each iteration, the current approximate eigenvalue is the length of b, and the current approximate eignevector is b normalized to unit length:
![]()
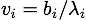
The next approximation for b is the matrix multiplication of M with the current eignevector:
![]()
Stop if the eigenvalue in any iteration is within 10-6 of the value in the previous iteration.
Measuring with valgrind
Compile your program as normal, then run using a command that looks something like this:
valgrind --tool=cachegrind --cache-sim=yes --branch-sim=yes program
There are two ways you could implement a matrix multiply for a symmetric matrix, either as
b[x] += M[x][y] * v[y]
or as
b[x] += M[y][x] * v[y]
Report the cache and branch statistics for both, using a matrix size of N=1000.
Submission
Submit your source code for both questions together with text output files for your testbench runs and cache and branch statistics. Also submit a text file named README that describes what files you have submitted for each question. Submit all materials by copying them to this directory on the GL server:
/afs/umbc.edu/users/o/l/olano/pub/611/$USER
Where $USER is your GL username.