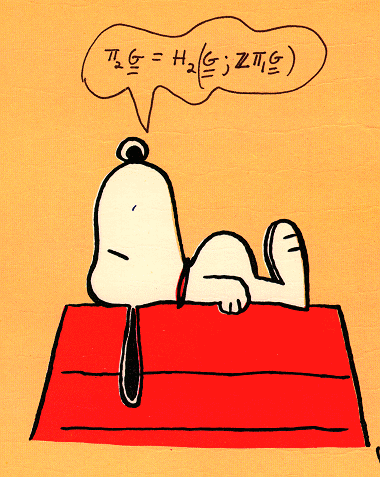Cartoon Based on the Following Papers

-
Five dimensional knot theory, in "Low Dimensional Topology,
"Contemporary Mathematics Series of the American Mathematics
Society, Providence,
Rhode Island, Vol. 20 (1984), pp 249 - 270.
-
The homotopy groups of knots I. How to compute
the algebraic 3-type, Pacific Journal of Mathematics, Vol. 95, No. 2
(1981), pp 349 - 390.
-
Homology of group systems with applications to low
dimensional topology, Bulletin of the American Mathematics Society,
Vol. 13, 3 (1980), pp 1049 - 1052.

 The fundamental group of a group system is
equal to the pushout of the group system.
The fundamental group of a group system is
equal to the pushout of the group system.
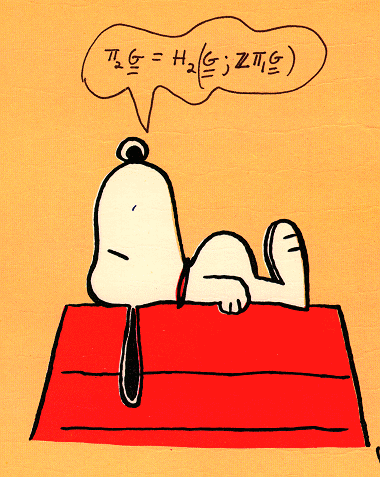 The second homotopy group of a group system is
equal to the second homology group of the group
system with twisted coefficients in the group ring
of the fundamental group of the group system.
The second homotopy group of a group system is
equal to the second homology group of the group
system with twisted coefficients in the group ring
of the fundamental group of the group system.
 The third homotopy group of a group system is equal to the
third homology group of the tensor product over G of the
group ring system with the second homotopy group of the group
system with twisted coefficients.
The third homotopy group of a group system is equal to the
third homology group of the tensor product over G of the
group ring system with the second homotopy group of the group
system with twisted coefficients.
 The second homology group of the group system with twisted
coefficients is isomorphic to the third homology group of the
pair (Pushout of the group system, group system) with twisted
coefficients.
The second homology group of the group system with twisted
coefficients is isomorphic to the third homology group of the
pair (Pushout of the group system, group system) with twisted
coefficients.
 The third homology group of the universal cover of a
Generalized Eilenberg MacLane (GEM) complex is isomorphic
to the third homotopy group of the group system of the GEM
complex with twisted coefficients.
The third homology group of the universal cover of a
Generalized Eilenberg MacLane (GEM) complex is isomorphic
to the third homotopy group of the group system of the GEM
complex with twisted coefficients.
 Oh, well ... !??
Oh, well ... !??