CMSC 635: Advanced Computer Graphics

Radiosity

Spring 1999

David S. Ebert
Computer Science and Electrical Engineering Department
University of Maryland, Baltimore County


Radiosity

(1984 Goral, et. al, at Cornell)

Cornell Box Radiosity simulation
Radiosity

Radiosity Equations

Radiosity * Area = Emitted energy + Reflected energy

Reflected energy = reflection coefficient * energy incident on the patch from all other patches.

Ei = light emitted from a patch (energy/time*area)

pi = reflectivity of the patch ( % of incident light reflected back into the environment). (rho)

FdAjdAi = form factor between patch dAj and dAi or % of energy leaving dAj incident on dAi.

This gives us:

displaymath172
OR
displaymath174

displaymath176

Form Factors:
displaymath178

displaymath180

So
displaymath182

displaymath184
Which can be rewritten as
displaymath186

Or the radiosity matrix


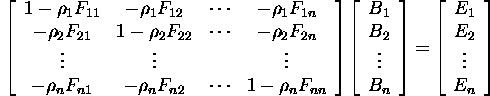displaymath188

where tex2html_wrap_inline190 and tex2html_wrap_inline192 are wavelength dependent.
displaymath194

displaymath196

tex2html_wrap_inline198 only for lights. tex2html_wrap_inline200 for convex surface.

Some Important Points to Note:

  • matrix diagonally dominant.

  • Can use Gauss-Seidel iteration to solve for Bi's

  • Matrix solution can be viewed at each iteration as gathering light in from all patches.

  • Bi's can then be used in renderer for illumination (color) at each patch n interpolated to average vertex intensities.

Radiosity Stages



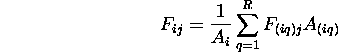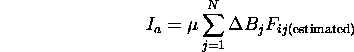
Computational Bottleneck: form factor calculations, O(n2)

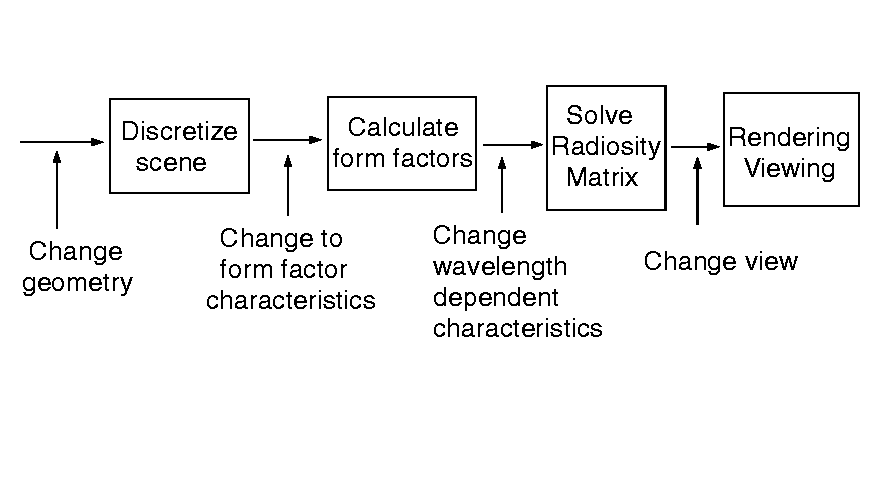
Discretization resolution determines accuracy of solution

  • need finer resulotion where radiosity gradiant is high

To increase accuracy, use

  • Substructuring: Patch (coarse) --> Elements (fine).

    Caculate Element-Patch form factors
    displaymath212
    where
    tex2html_wrap_inline214 F.F. from patch i to patch j
    tex2html_wrap_inline220 F.F. from element q of patch i to patch j
    tex2html_wrap_inline228 area of element q of patch i
    R = # of elements in patch i.

-- now have tex2html_wrap_inline238 form factors

Calculating element radiosities
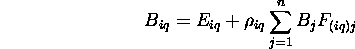
displaymath240
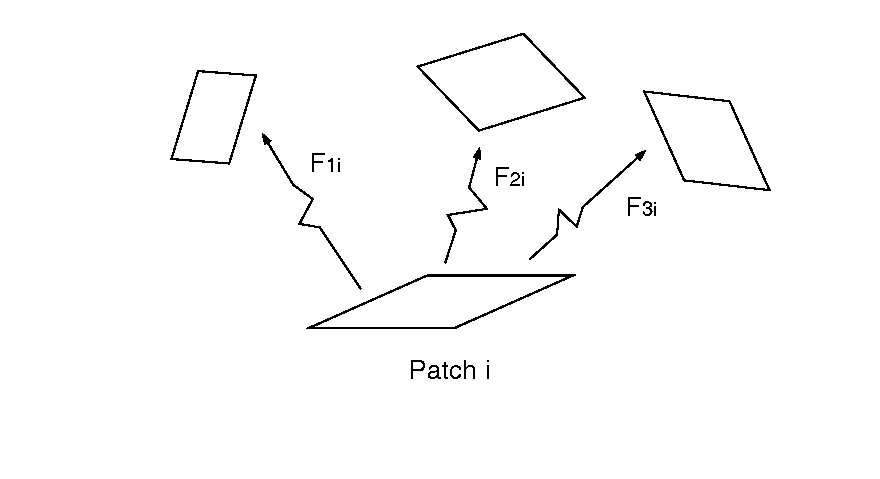
for an element, only look at other patches, not elements.

Resulting operations needed:

  1. Calculate patch form factors.

  2. Calculate patch-patch coarse solution.

  3. Subdivide patches into elements based on gradiant and calculate element-patch F.F.

  4. Calculate element radiosities.

Progressive Refinement

  • Progressively increase the realism.

  • In traditional ``gathering'' method, a solution for one row produces the radiosity for a single patch
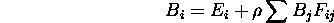
    displaymath242
    Estimate of radiosity of patch i based on current value of all other patches.
    ==> gathering illumination.

  • shooting method -- At each step, radiosity from a patch is shot onto all other patches ==> entire image gets better at each step.



    For all j:
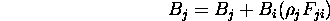
    displaymath252
    where 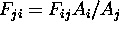tex2html_wrap_inline254.

Shooting Algorithm 


Repeat 
 
    For each Patch i 
 
        for first iteration calculate F.F. 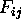tex2html_wrap_inline258.
 
            For each Patch j (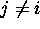tex2html_wrap_inline262) 
 
                { 
 
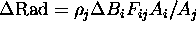
                tex2html_wrap_inline264
 
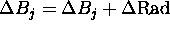
                tex2html_wrap_inline266 
 
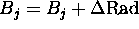
                tex2html_wrap_inline268 
 
                } 
 
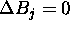
            tex2html_wrap_inline270 
 
Until convergence

Improvements:

  1. Order patches by 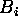tex2html_wrap_inline206, so shoot brightest patches first.
  2. Add an ambient approximation
    • to keep illumination of scene nearly constant
    • descrease as solution gets more accurate
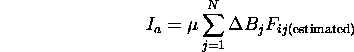
      displaymath274
      where 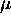tex2html_wrap_inline276 is the overall reflection factor.

Form Factor Issues

  1. high cost to compute -- nontrivial
  2. Fij also must look at all other patches (shadowing/blocking).
    hemicube solves 1 & 2 together.



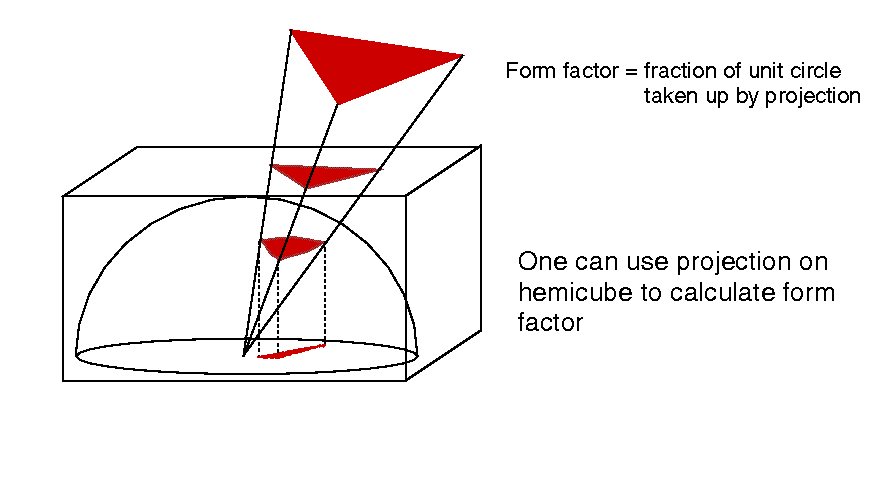
    Form Factor = fraction of unit circle taken up by projection.

  3. Gathering algorithm requires storage and calculation of form factor matrix
    tex2html_wrap_inline202 large storage for matrix.

Return to CMSC 635 Notes Page

Last modified: Mon Mar 1 15:20:54 EST 1999