CMSC 635: Advanced Computer Graphics

Transparency and Shadowing

Spring 1999

David S. Ebert
Computer Science and Electrical Engineering Department
University of Maryland, Baltimore County


Transparency




n1 / n2 = sin ( thetat ) / sin( thetai )

Basic Equations:

Reflected Light: R = 2(N*L)N - L

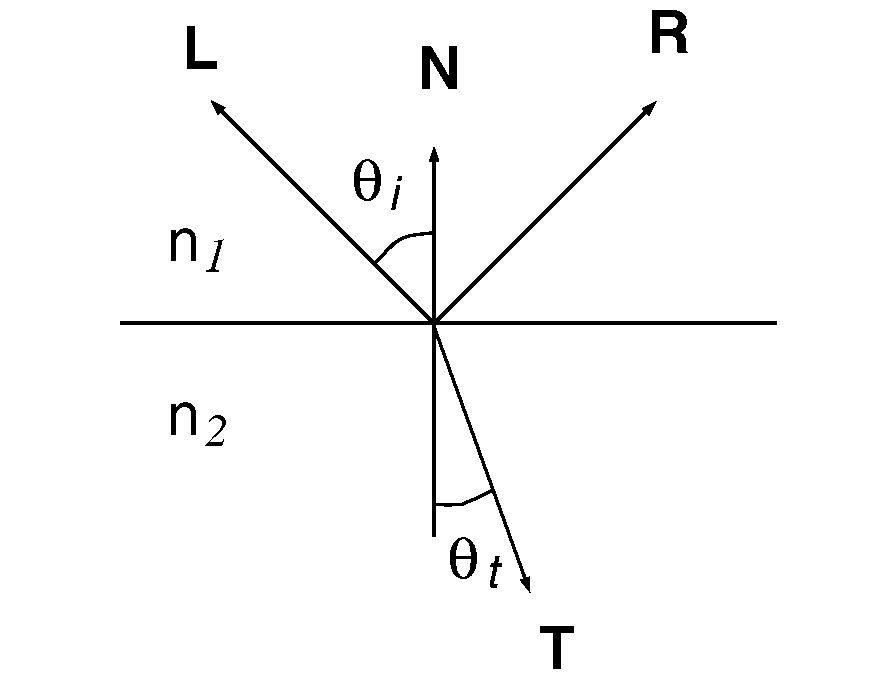
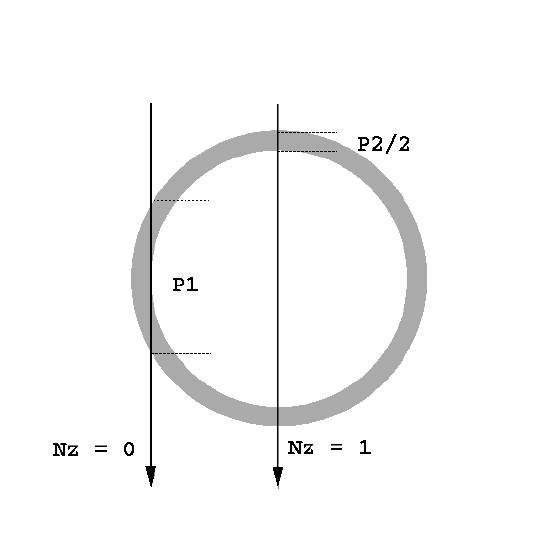Transmitted Light: T = (n1 / n2 ) L - [ cos(thetai) + (n1/ n2)(N*L) ] N

How does this get added in to the color calculation?

  1. Hall
    - Add a term to the illumination equation:
    I = ... + kt(N * H')n
    H' = [ L - ((n1 / n2 ) V]
    /(n1 / n2 ) -1]

  2. Kay
    - No refraction
    - Blend background color

    -Simple version: I = tIbackground + (1 - t)Iobject
    where t is % of transparency.

    - Complex version:
    Simulate a curved hollow surface -> less transparency at edges because more material (P1 >> P2) :

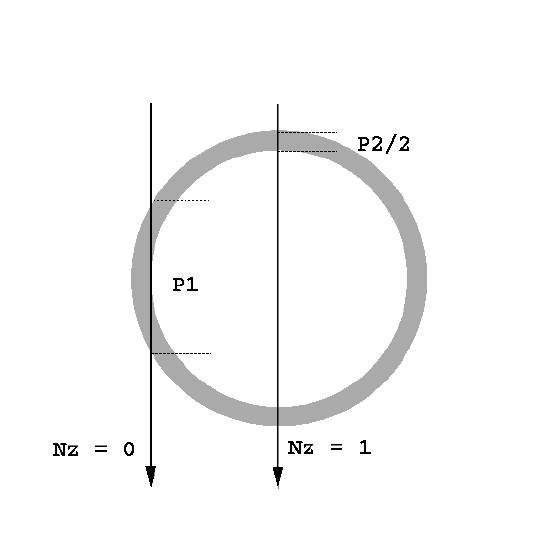
    Modulated by Nz -- z-component of normalized normal of the projected object, one has
    t = tmin + (tmax - tmin)Nz

    For smooth shading, go through more and more material, so raise to a power. Final Formula:

    t = tmin + (tmax - tmin)[1 - (1-Nz)P]

    Only works with some hidden surface removal algorithms

    How can this work with a Z-buffer algorithm?

    What about specular highlights ?

    -- Should wash out transparency

    I = (specular of transparent surface) + (1 -t)*(ambient+diffuse of transparent surface) +
    t*(rgb of background)

    ==> %opaque = (1-t) + %specular

    How can you add refraction ?

SHADOW GENERATION

Definitions

umbra
portion completely hidden from light -- darkest area

penumbra
  • can partially see light
  • only present with a distributed light source -- ``soft shadow'' area

We will look at algorithms mainly concerned with point light sources.

Algorithms

  1. During scan-out: SHADOW EDGES


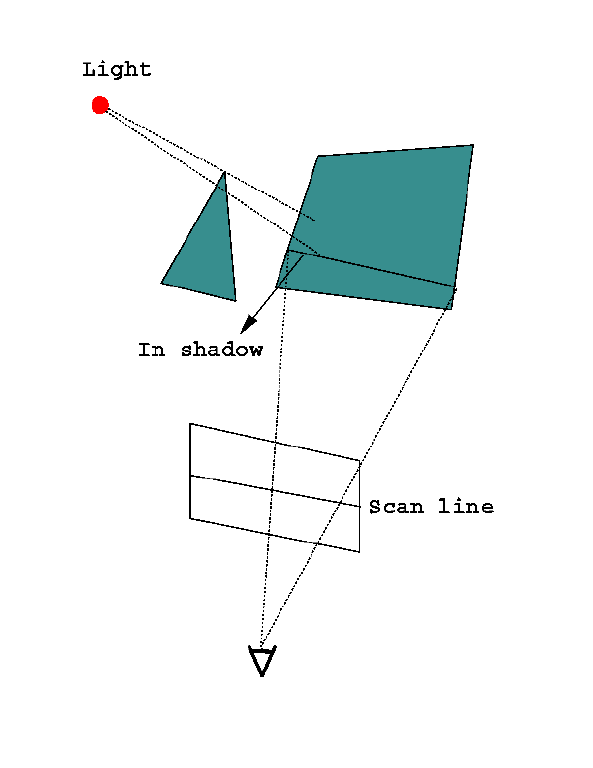
    1. pre-process to determine which polygon can shadow each polygon.
    2. During scan-out:
      1. if no shadowing polygon, just do standard illumination.
      2. if shadowing polygons
        • if doesn't overlap current segment, just do normal illumination.
        • if completely covers this segment, shadow it
        • else, subdivide and test each area.

    • tricky algorithm
    • extra data structure
    • uses span coherence
    • depends on observer position
    • lots of calculation during scan-out

  2. Shadow polygons (Atherton, Weiler and Greenberg 78)

    • two pass algorithm
    • Pass 1 calculates shadow polygons by doing H.S.R. w.r.t. light source (Weiler-Atherton alg.).
    • Pass 2 H.S.R. combined with shadow polygons. Polygons without attached shadow polygons should be darkened.
    • view independent
    • object space resolution
    • increases storage space for shadow polygons.
    • break polygons based on shadowing information

  3. Shadow Volumes (Crow 77)

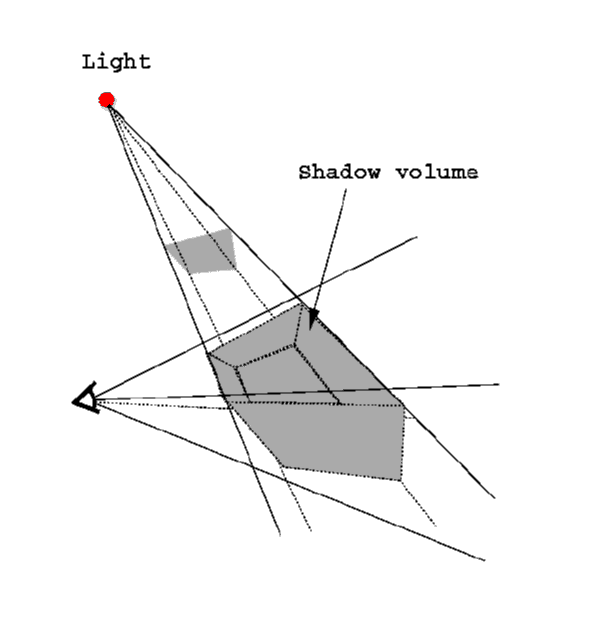
    • common algorithm
    • creates shadow volumes resulting from silhouette edges of object and light source.
    • shadow volume formed by shadow polygons. Each shadow polygon is tagged with the shadow volume, light sources and forward or backward to the eye.
    • during scanning each pixel
      • a counter for each light initialized to 1 (if eye in shadow) or 0 (if otherwise)
      • process depth sorted polygons
        • for shadow polygons
          • if front, counter[l] += 1
          • if back, counter[l] -= 1
        • for normal polygons
          • if counter[l] even, not in shadow
          • if counter[l] odd, in shadow

    Problems with shadow volumes:

    • adds a lot of polygons
    • non-trivial to generate shadow volume and polygons.
    • need depth sort

    Advantages with shadow volumes:

    • independent of observer position
    • efficient
    • extendible to penumbra through creation of multiple shadow volumes
    • light volumes -- lights create illuminated volumes as well as shadow volumes

  4. Shadow Z-buffer (image space)


    • create shadow maps (depth buffer) by using Z-buffer algorithm with each light being the eye point.
    • during normal Z-buffer scanning 

            if Pz < Z_buffer[x][y]
         for each light
            transform Pz to light coordinates Pz'
            if Pz' > L_buffer[x'][y']
               P in shadow
            else 
               P not in shadow

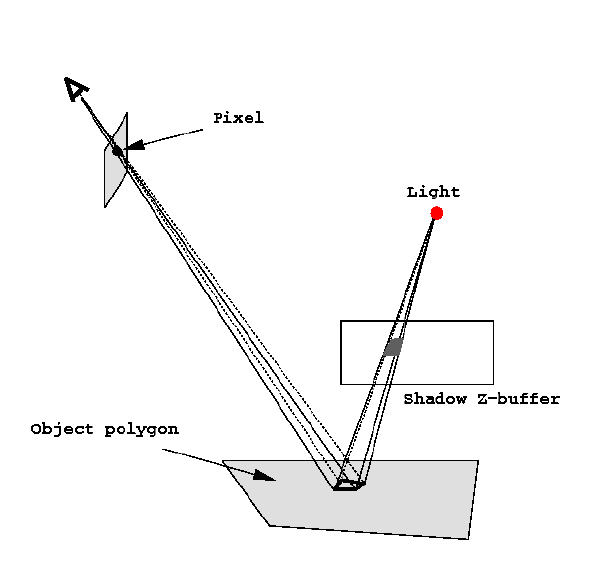
    Advantage

    • easiest to implement

    Disadvantages

    • aliasing, using lots of memory
    • perspective distortion

    More problems with shadow maps

    • point sampling gives errors
    • how to integrate shadow area
      • do binary decisions, then average to give % in shadow call ``percentage closer filtering''.

  5. Raytraced soft shadows
    • shoot multiple rays sampling the area of the light source
    • jitter rays to reduce aliasing

  6. Shadow tables (Kajiya 84, Ebert 90)
    • Surround each object with 3D lattice. Compute shadowing incrementally from light source -- wave propagation.
    • 3D table for each object for each light
    • During scan out, shoot ray to light and see where intersects table which cell's face, interpolate shadow values.
    • volumetric shadowing method
    • Could extend to light volumes
    • extend to polygons

  7. Fake shadows
    • project object onto plane using light for perspective point.

Return to CMSC 635 Notes Page

Last modified: Sun Feb 21 17:43:41 EST 1999