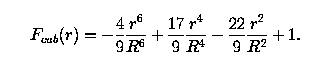CMSC 635 Spring 1999 - Advanced Modeling

CMSC 635: Advanced Computer Graphics

Introduction to Advanced Modeling Techniques

Spring 1999

David S. Ebert
Computer Science and Electrical Engineering Department
University of Maryland, Baltimore County


Traditional Geometric Representations

Advanced Modeling Techniques

Fractals:

L-systems

  • Authors: Lindemyer & Prusinkiewicz, Alvy Ray Smith, Fowler

  • Rule based grammers for describing natural objects

  • Great for plants, trees, shells

  • Example: 

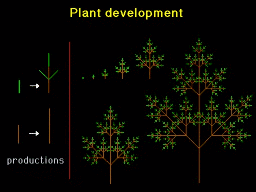
  • Simple Example of a another tree created by the following production rule:


    • a -> a[+a]a[-a-a]a


    with initial axiom a


  • All rules applied simultaneously.

  • Also probabilistic and context-sensitive L-systems.

  • Most recent work is on Open L-systems that react to their environment.

  • See also the work by Prusinkiewicz & Hammel

  • Examples

    Green coneflower. Copyright © 1992 D. Fowler, P. Prusinkiewicz, and J. Battjes.

    A Horsechestnut tree model with branches competing for access to light, R. Mech and P. Prusinkiewicz. Copyright © 1996 P. Prusinkiewicz.

    A model of coniferous trees competing for light. The trees are shown in the position of growth. R. Mech and P. Prusinkiewicz. Copyright © 1996 P. Prusinkiewicz.

    A model of coniferous trees competing for light. The trees are moved apart from the position of growth. R. Mech and P. Prusinkiewicz. Copyright © 1996 P. Prusinkiewicz.

Particle Systems


Image from Star Trek II: The Wrath of Khan by Pixar, copyright © 1987 Pixar.


What are Particle Systems?

A large collection of (normally) very simple geometric particles
that change stochastically over time.

Introduced to computer graphics by Bill Reeves in 1983

Allow a few parameters to control a complex, dynamical system (data amplification)

An example of procedural animation --
    animation, location, movement, birth, and death of
    parcticles are all controlled algorithmically.

Commonly used to represent natural phenomena, such as
steam, smoke, fire, water, snow, rain.

Three main components of a particle system:
  • particle representation and geometry
  • particle dynamics
  • particle rendering

Particle Attributes (Representation and Data Structures)

  • geometry /shape (radius)
  • color
  • opacity
  • position (initial)
  • velocity
  • lifetime

Particle Dynamics

Governs how the particles move from frame to frame

Often represented as forces
  • Gravity
  • Air resistance
  • Attraction
  • Repulsion
  • Collision (with objects only)
  • Wind Fields
  • Turbulence Fields
  • Stochastic functions
  • Vortices (Sims 90)
  • Navier-Stokes Flow equations

Particle Rendering

Problems because of the large number of primitives
     (hundreds of thousands to millions

Simple Method:
  • Consider each particle as a point (linear if motion-blurred) light source.

  • The color of the particle is constant and unshaded.

  • Accumulate the contribution of each particle into the frame-buffer

  • composite with the normally rendered scene.

  • No occlusion, no inter-particle illumination

Structured Particle Systems (Reeves and Blau 85)
  • Probabilistic rendering techniques to speed rendering.

  • Perform hidden surface removal, illumination, and shadowing for the particles.

  • Usually modeling stochastic phenomena, so rendering can be
          approximately correct.

  • Perform approximate/probabilistic illumination.
          (e.g., distance into tree from light source determines diffuse shading
          and probability of having specular highlights, etc.)
  • Perform approximate/probabilistic shadowing -
          exponentially decrease ambient illumination as depth into structure increases.

  • External shadowing also probabilistically approximated.

  • For hidden-surface removal, use a painters algorithm along
          with a depth-bucket sort of particles.
          Won't be correct in all cases, but approximately correct.

    Example from Andre and Wally B (Pixar)

    Example from Road to Point Reyes (Pixar)

Particle System Operation

  • New particles are generated and assigned initial attributes

  • Particles past their lifetime are removed

  • All remaining particles are updated based on dynamics and

    procedures

  • Particles are rendered, often using special purpose algorithms

Advanced Particle Systems

  • Structured Particle Systems

    • Particles form a connected, cohesive 3D object and have inter-particle relationships.
    • Used to model trees, plants, etc., so similar to probabilistic, context-sensitive L-systems

    • Unlike L-systems, goal is to model appearance of collections of trees, plants, etc.

    • Construct trees, by recursively generating sub-branches with stochastic variation of parameters.

    • Therefore, a few parameters generate an entire forest.

    • Each particle represents an element (branch, blade of grass, etc.)

  • Cloth dynamics based on particle systems (Breen 1994, Maya cloth, Witkin and Baraff 1998)

  • Surface modeling with oriented particle systems (Szeliski and Tonnenson)

  • Complex geometry and implicits attached to particles - clouds, etc. (Ebert, Stam)

Common Issues

  • Rendering still difficult

  • Inter-particle interactions - how to efficiently handle this

  • How much physics vs. how much user control

  • The perilous power of parameterization

  • Diffusion Limited Aggregation (DLA)
    • Natural process hypothesized to describe how many natural things form,

      • including dendrite clusters to the formation of galaxies.
    • Based on random walks (fBm motion) of particles.
    • Several initial sticky particles are placed in space.
    • A large number of additional particles are moved on random walks;
    • if they touch one of the sticky particles, they stick and may become sticky also.
  • See also Rick Parent's chapter on Particle Animation

    • Procedural Models

    • Authors: Ebert, Perlin, Hart, Musgrave

    • Use algorithms, code segments, procedure to define the geometry of your object.

    • Add as much physics or art as you want

    • Advantages: flexibility, data amplification, procedural abstraction.

    • Examples:

      • Volume metaball Cloud  This image is a volume rendered and procedural altered metaball. The image has low-albedo gas illumination and atmospheric attenuation.


        •  

         

      • My version of the blizzard of '96  This image shows how metaballs, volume swirling snow, and polygonal models can be combined to produce great images. You could say that during the blizzard I created a virtual snowman and my own blizzard.


        •  

         

    Implicit Models
    • Authors: Wyvills, Hart, Blinn

    • Describe objects with implicit equations: F(x,y,z)=0

    • Blend objects together using smooth function: 


      • R = distance where function has a value of 0.
       
       

    • Graph of Blending Function: 

    • Create iso-surface of blended density fields.

    • Example: 10 Years of Implicit Surfaces by Brian Wyvill 

    • Common Example effects: liquid metal creature from Terminator 2, flubber, klingon blood

    • Images courtesy of Brian Wyvill (blob@cpsc.ucalgary.ca).

    Return to CMSC 635 Notes Page