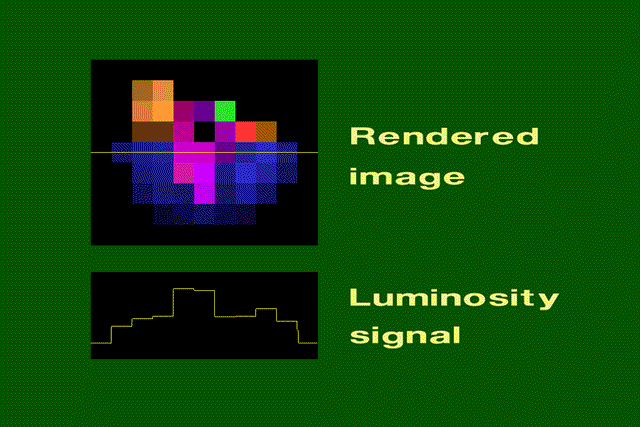CMSC 635 Spring 1999 - Anti-Aliasing

CMSC 635: Advanced Computer Graphics

Introduction to Aliasing and Anti-Aliasing Techniques

Spring 1999

David S. Ebert
Computer Science and Electrical Engineering Department
University of Maryland, Baltimore County



Why does Aliasing Occur?

Discretely sampling a continuous signal/function/object.

Two components: Sampling and re-construction


Where does Aliasing Occur?

  • Motion - popping/flashing/strobing
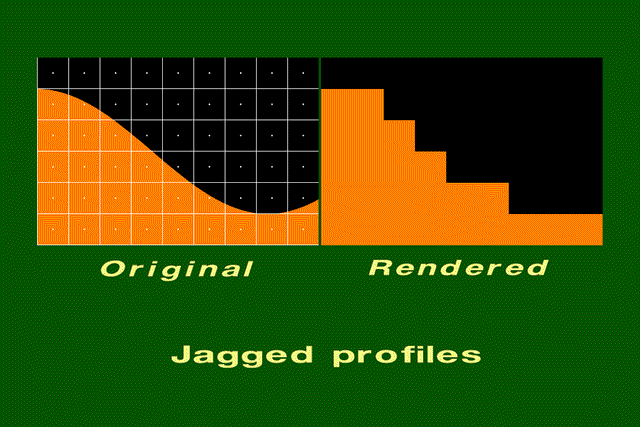
  • Edges - jaggies
  • Textures - crawling/ Moire patterns
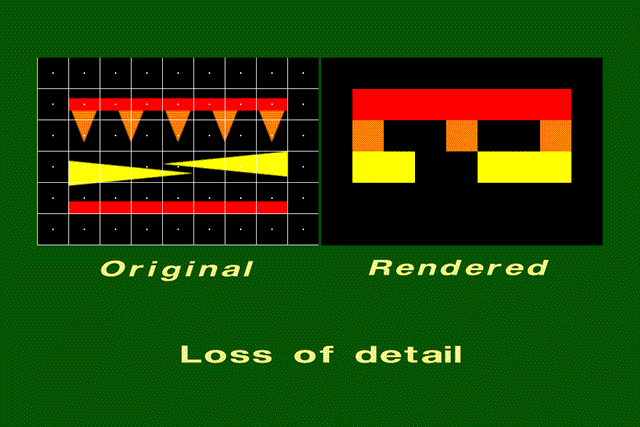
  • Missing details in textures, geometry


    An Illustrated Example: A Spinning Cylinders

    Example animation


    Spinning cylinders starting position.


    Spinning cylinders after 1/24 second.

    What is going on?

    Rotation Rate 0/24 second 1/24 second 2/24 second
    3 rps 0 deg. 45 deg. 90 deg.
    5 rps 0 deg. 75 deg. 150 deg.
    11 rps 0 deg. 165 deg. 330 deg.
    12 rps 0 deg. 180 deg. 360 deg.


    Sampling: How frequently should we sample?

    • Too much -- waste of time

    • Need to sample the signal frequently enough to be able to reconstruct it correctly.

    • Too little (undersampling) -- lose information --> aliasing

    • Undersampling can cause the signal to appear as a lower frequency signal - it aliases

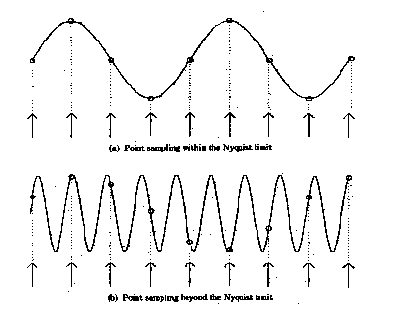
    • Need to sample the signal at least at twice it's frequency (Nyquist Criteria)

    Example of 1D aliased sampling:


    Sampling Theory

    • Shannon's Sampling Theorem:
      A continuous bandlimited function of a single variable can be completely represented by a set of samples made at equally spread intervals. The interval between samples must be less than half the period (or greater than twice the frequency) of the highest frequency components in the spectrum (called the Nyquist Limit).

    • Brief overview of Fourier Synthesis

      Any signal can be represented as a series of sine waves of different frequencies.

      Fourier transformation pair:
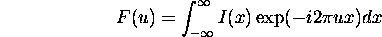
      displaymath48

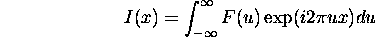
      displaymath50

      F(u) is the sum of sine waves because
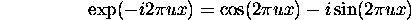
      displaymath54
      u = frequency of sine wave -- frequency domain
      x -- spatial domain

    • Convolution
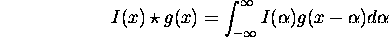
      displaymath56

      if I(x) -> F(u) and g(x) -> G(u)
      I(x) * g(x) -> F(u)G(u) (convolve in spatial, multiply in frequency domain)
      I(x)g(x) -> F(u) * G(u) (multiply in spatial, convolve in frequency domain)

      So, to create frequency representation of the function, multiply by reconstruction filter ==> original frequency function of the signal.

      No information lost iff
      displaymath72
      or
      displaymath74

      where x is sampling rate and 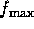tex2html_wrap_inline78 is the Nyquist Limit.

    • Aliasing occurs when
      • I is not bandlimited -- can't solve this

      • Sampling rate is not high enough for a bandlimited function, frequencies f > fs/2 tex2html_wrap_inline80 will be lost.
      • In Graphics, there are 2 (or 3) dimensions:
        displaymath82

        displaymath84

    • Common Aliasing Solution:

      Super-sampling: sample x times / pixel

      • Does this solve the problem?

        Example: Solid Texturing 

        	If(x % .5) < .25
		color = black
	else 
		color = white
      • Problems:
        • doesn't solve problem, just raises Nyquist limit
        • can only decrease resolution so much


    Reconstruction/Filtering:

    • How do you combine the samples to get the original signal back?

      Equal weights (square filter)
      Center weighted (pyramid)
      Gaussian
      Example

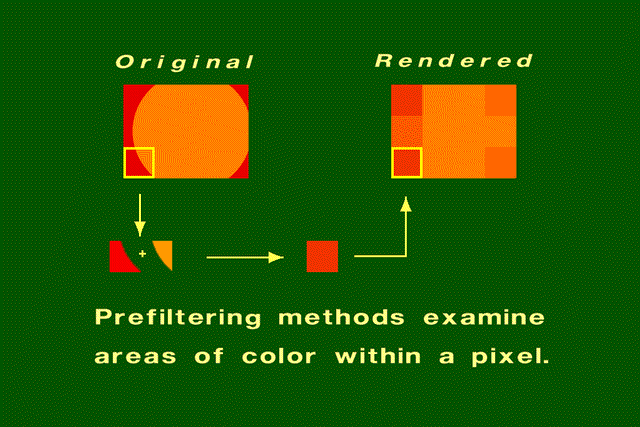
    • Pre-filtering

      Consider pixel as area and integrated contribution to that pixel

    • Post-filtering

      Sample the pixel and then reconstruct the samples (filter) to get pixel value

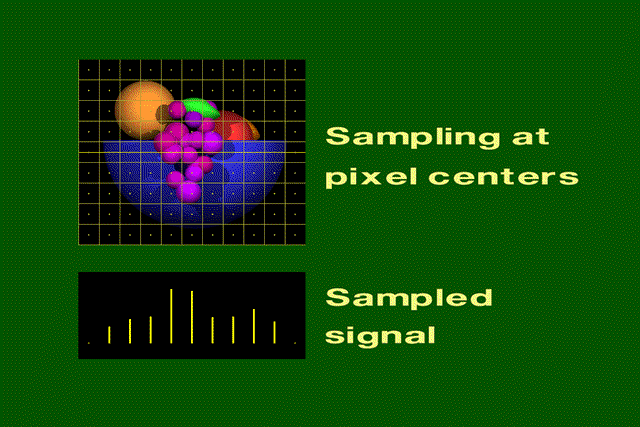
      Ordered sampling/regular sampling - use pre-defined grid

      Stochastic sampling - sample randomly

      Jittered sampling (Cook) - stochastically jitter the regular sampling grid

      Human eye finds noise less objectionable/noticable
          => trade noise for aliasing artifacts

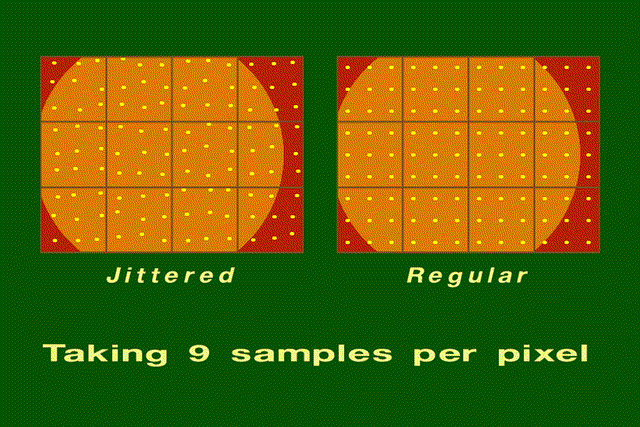
    • Examples:

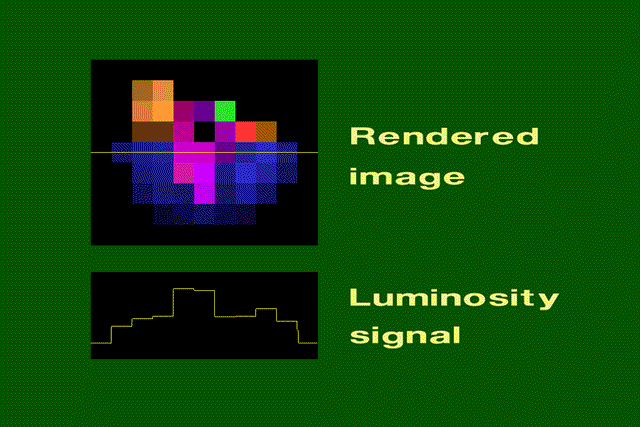
    Example Controls in a Commercial Package: Maya

    • Anti-aliasing
      low-quality - 2 samples per pixel
      med-quality - 8 samples per pixel
      high-quality - 32 samples per pixel
      highest-quality - 32 samples per pixel in pass 1, look for high contrast areas and resample them to get better resolution

    • Texture Maps
      Mip-map - store at various levels of detail (pre-filtered texture maps)
      Others - filters from simplest to most accurate

    • Shading anti-aliasing
      Multi-pixel filter - Looks at 3x3 pixels and filters them
      Shading samples - number of samples for each pixel fragment
          for shading computations
      Max shading samples - for 2nd pass of Highest quality
      Particle samples - same as shading samples
      Motion blur - number of time samples made

    • Procedural Texture aliasing
      choose filter size
      control number of iterations and frequencies you allow into it.

    Antialiased texture mapping

    • Covered before (see Texture mapping notes)

    Return to CMSC 635 Notes Page