David S. Ebert
September 2000




Surfels
Fractals:
Sierpinski - Start with filled
equalateral triangle. Connect midpoints of each side, remove middle
triangle, repeat.
von Koch, etc. - Start with line,
divide into 1/3s, replace middle 13 with 2 edges of right triangle,
repeat.
Multi-fractal landscape
Lava Landscape
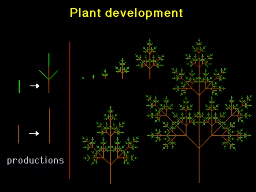
L-systems
A Horsechestnut tree model with branches competing for access to
light, R. Mech and P. Prusinkiewicz. Copyright © 1996
P. Prusinkiewicz.
A model of coniferous trees competing for light. The trees are shown in the
position of growth. R. Mech and P. Prusinkiewicz. Copyright © 1996
P. Prusinkiewicz.
A model of coniferous trees competing for light. The trees are moved
apart from the position of growth. R. Mech and
P. Prusinkiewicz. Copyright © 1996 P. Prusinkiewicz.
Procedural Models
 Image from
MERL
Image from
MERL
The Mandelbrot set:
Fractal Mountains:
Examples Landscapes from F. Ken Musgrave



a -> a[+a]a[-a-a]a
with initial axiom a




 This image is a volume rendered and procedural altered metaball. The image
has low-albedo gas illumination and atmospheric attenuation.
This image is a volume rendered and procedural altered metaball. The image
has low-albedo gas illumination and atmospheric attenuation.
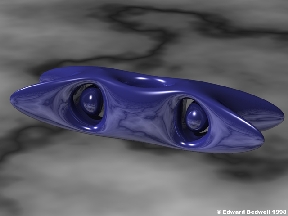
Implicit Models
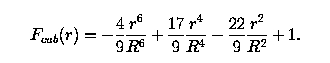
R = distance where function has a value of 0.