- Ray Casting (Simplest Image Space Algorithm)
- Basic Object Space Algorithm:
- for each pixel
- Determine the closest object along the ray from the eye
pt. through the pixel.
Find it's color
Set pixel color to this color.
- For each object
Determine the visible surfaces of the object
(those portions that are unobstructed in the
view)
- Find their color Draw them.
- Painter's Algorithm
- Sort all the polygons in the scene in Z depth.
- For poly = farthest to closest
- This works fine unless 2 polygons that
- Basic idea
- Problem Cases:
Find the color of poly.
Draw it on the screen.
overlap in x & y also overlap in Z.
Then need subdivision or some other
technique.
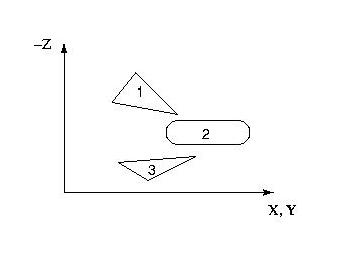
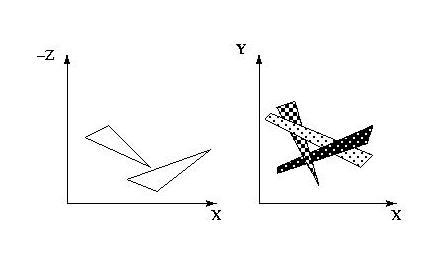
- We know how to scan-convert polygons onto the screen.
- What we want to do now is, only overwrite a pixel if the polygon element has a larger Z value than what is in the frame-buffer currently.
- We will create a Z-buffer to hold the depth values of each pixel in the frame-buffer.
- The general Algorithm:
- Initialize frame-buffer and Z-buffer
for each polygon P
polycolor[x][y] = color of P at this pixel
if Z-buffer[x][y] <= pz
Z-buffer[x][y] = pz
FB[x][y] = polycolor[x][y]
end for each pixel
end for each polygon
- Z values calculated incrementally from the plane equation (dz/dx, dz/dy).
- Number of comparisons independent of number of polygons.
- Works fine for patches & other primitives.
- Requires a large amount of memory ??
-
Often implemented in hardware.
- (1280*1024*32bits typically > 5Mb)
- Instead of storing an entire Z-buffer, what if we store only 1 scanline at a time to save memory ?
- How does the algorithm have to change?
- We switch the order of the for loops.
- Initialize scanline color-buffer CB and Z-buffer
for each polygon P active in the scanline
for each x in poly's projection
pz = the Z value of P at this pixel
- polycolor[x][y] = color of P at this pixel
Z-buffer[x] = pz
CB[x] = polycolor[x][y]
end for each x
end for each polygon
draw the color-buffer CB to the screen
end for each scanline
- What are the disadvantages of this algorithm compared to the Z-buffer algorithm?
- Screen-Space Subdivision.
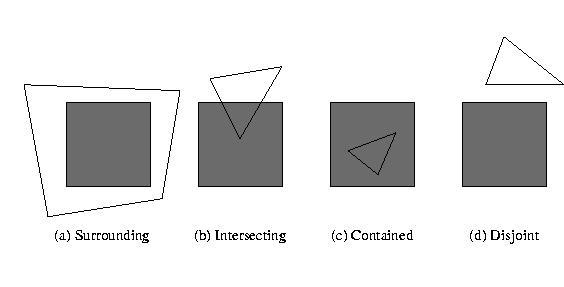
- A polygon's relation to an area is one of 4 cases:
- Completely surrounds it.
- Intersects it.
- Is contained in it.
- Disjoint (is outside the area)
- If one of the four cases below doesn't hold, then subdivide until it does:
- All polys are disjoint wrt the area =>
- 1 intersecting or contained polygon =>
- There is a single surrounding polygon =>
- There is a front surrounding polygon =>
- Recursion stops when you are at the pixel level, or lower for anti-aliasing.
- At this point do a depth sort and take the polygon with the closest Z value.
- Most of the work is done at the object space level.
- An Example:
- draw the background color
- draw background, then draw contained portion of the polygon.
- draw the area in the polygon's color.
- draw the area in the polygon's color.
Illumination Models
- the lights, the observer position, and the object
characteristics determine its final brightness and color.
- Color, Intensity, Direction, Angle of illumination, geometry
- The light that is the result from the light reflecting off other surfaces in the environment that strikes all the surfaces in the scene from all directions
- This is independent of direction:
- The equation for the amount of light received by a surface is therefore:
- Ia is the intensity of the ambient light in the scene.
- ka is the ambient-reflection coefficient which determines the amount of ambient light reflected from a given surface. 0 <= ka <= 1.
- I = Iaka
- This simulates thedirect illumination that an object receives from a light source that it reflects equally in all directions.
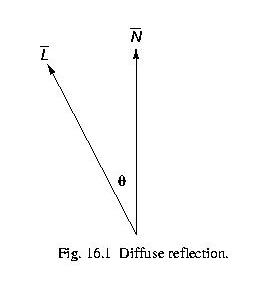
- Dull surfaces exhibit diffuse reflection, also called Lambertian Reflection from Lambert's Law.
- Brightness of object is independent of observer position (reflect equally in all directions).
- Diagram of geometry
- Lambert's Law: Id = Ipcos(q)
- Id = Ipkd (N * L) if N & L are normalized, 0 <= k <= 1
- where Ip is the point light source's intensity.
So combined,
- I = Iaka + Ipkd (N * L)
- These are those bright spots on objects (hot spots)
- If you look around, these move as you move around.
- Therefore, specular reflection is dependent on the observer position.
- We will use the formulation that has H, the half-angle vector. Also called the direction of maximum highlights.
- If the normal is alligned with H, you will have maximum highlights. As you move away from this, it will decrease.
- Phong's model:
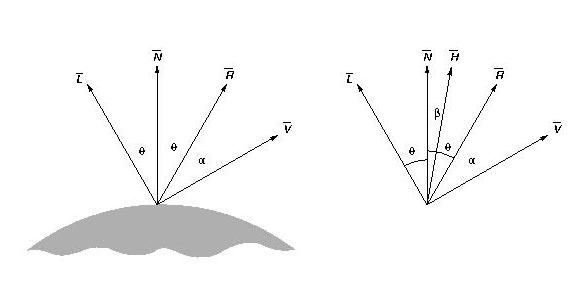
- H = L+V, normalized,
- Is = ks(N*H)n
0 <= ks <= 1, property of the material
n <= 1. Good choice is 50.