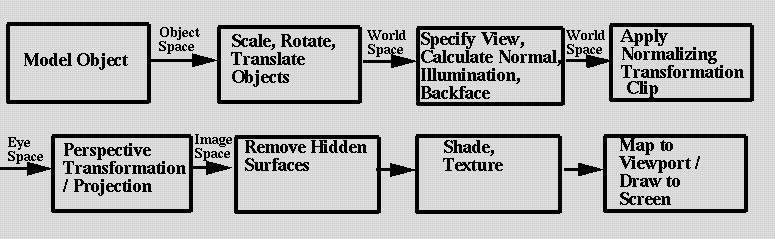
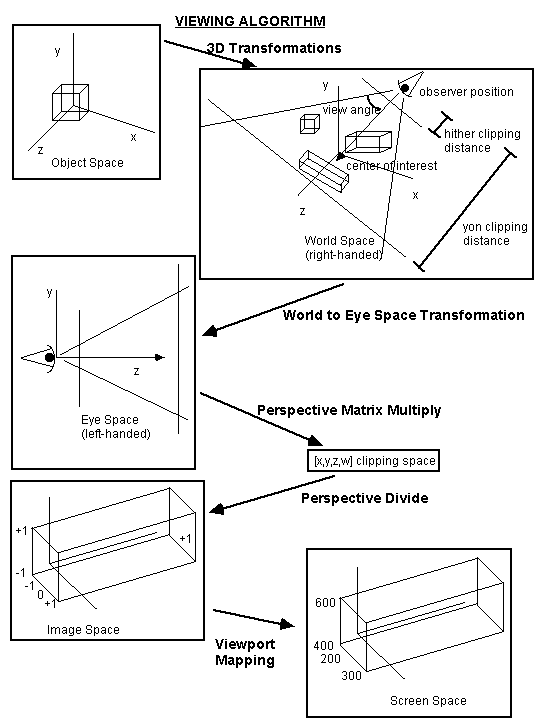
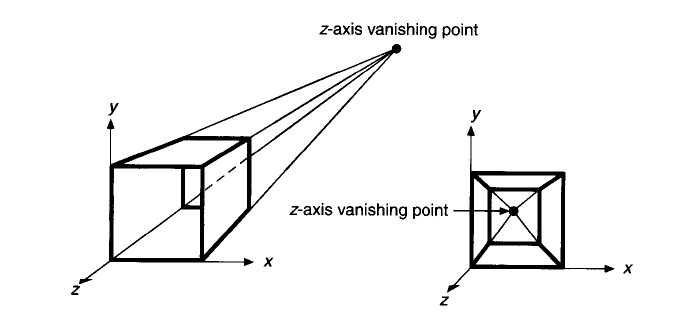
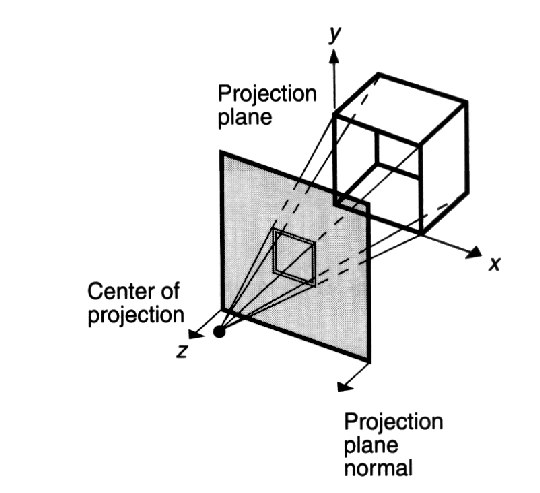
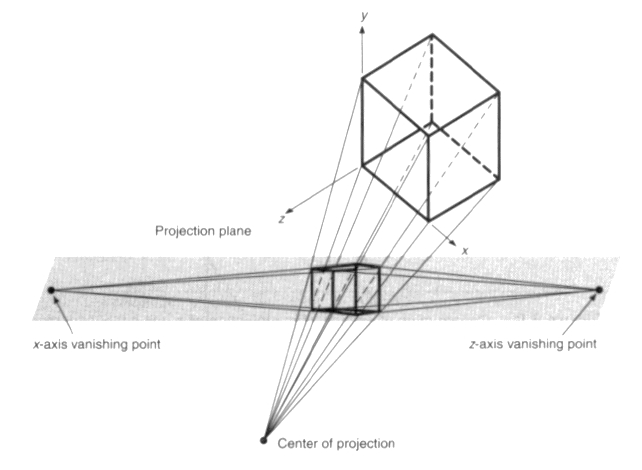
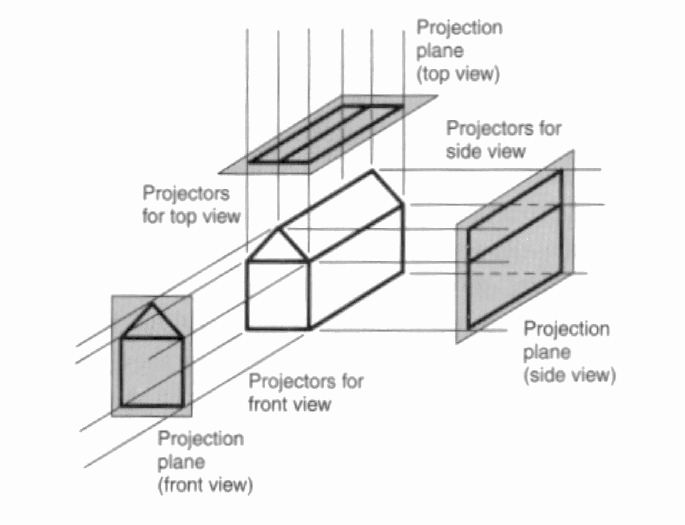
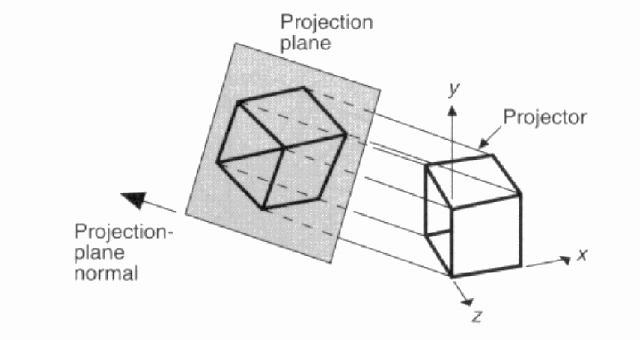
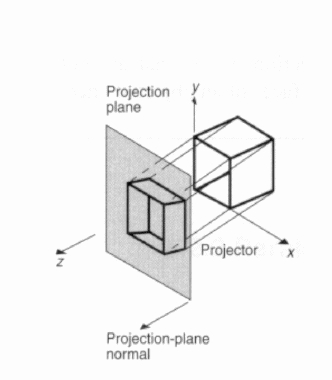
Right Handed Space Left Handed Space
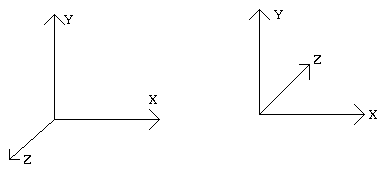
- |x|
|y|
|z|
|1|
Right Handed Space Left Handed Space
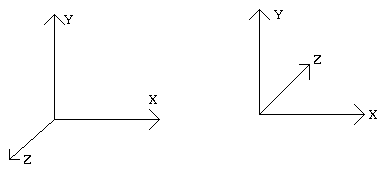
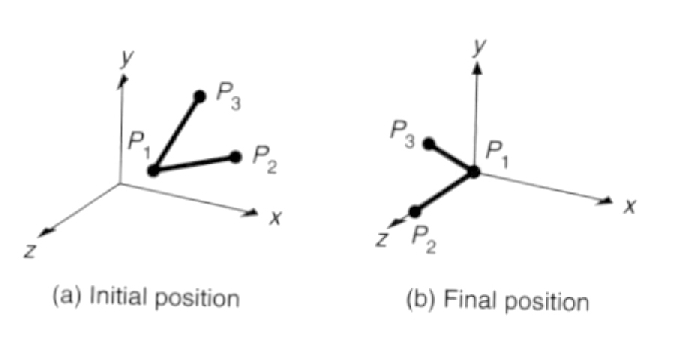
4 Steps:
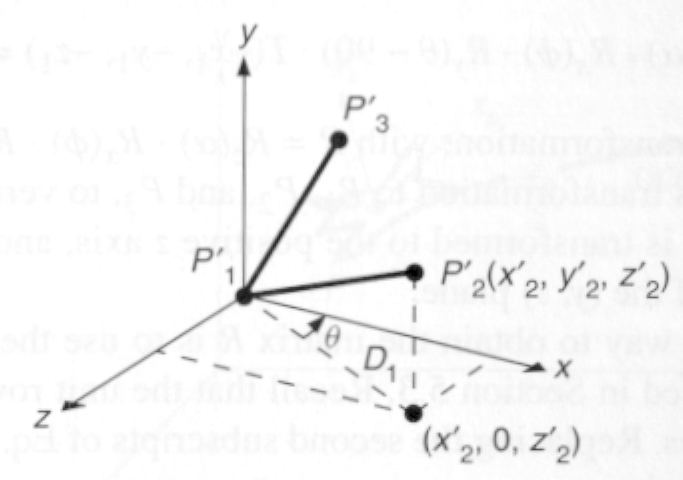

2) Next, we rotate the axis into one of the principle axes, let's pick Z (|Rx|, |Ry|).
3) We rotate next by d degrees in Z ( |Rz(d)|).
4) Then we undo the rotations to align the axis.
5) We undo the translation: translate by (x0,
y0, z0)
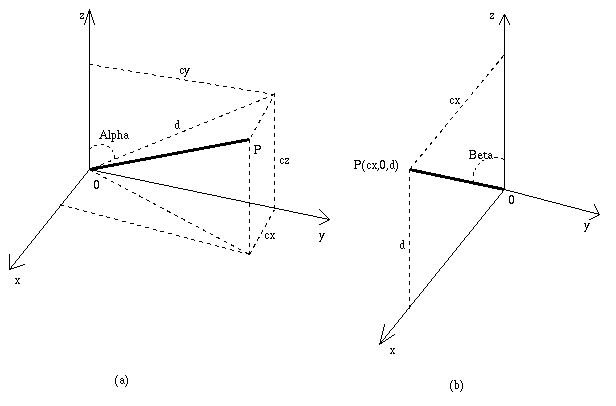
Similar to above:
cx = (x1 -x0)/ |V|
cy = (y1 -y0)/ |V|
cz = (z1 -z0)/ |V|, where |V| is the length
of V