REGION FILLING

Connectedness:

4-connected region: from a given pixel you can get to any other pixel in the region by a series of 4 way moves (up, down,left, right).

8-connected region: from a given pixel you can get to any other pixel in the region by a series of 8 way moves (up, down,left, right, up-left, up-right, down-left, down-right).

Note:

1) An 8-connected boundary defines a 4-connected region

2) If something is 4-connected, it is also 8-connected.

Interior vs Boundary-defined.

An interior defined region is the largest connected region of points that have the same value.

A boundary defined region is the largest connected region of points that do not have the boundary value.

Examples:

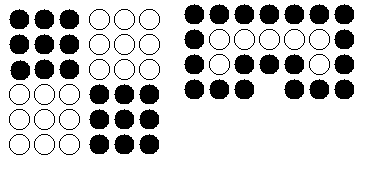
The algorithms we will look at:

1) Seed fill (Flood fill)

2) Scanline-seed fill

3) Scanline fill

1 &2 work at the pixel level, 3 works at the polygon level.

What advantages are there to work at each of the levels?

1) Seed Fill

Can work on interior or boundary defined regions.
Start with a seed point inside the region.
If the point is not already set to on,turn it on & visit the 4 neighbors of the point recursively.
Flood fill algorithm (interior-defined)

        Flood-Fill(x,y, oldvalue, newvalue)
                if (get_pixel(x,y) = oldvalue)
                        plotpoint(x,y, newvalue)
                        Flood-Fill(x+1,y)
                        Flood-Fill(x-1,y)
                        Flood-Fill(x,y+1)
                        Flood-Fill(x,y+1)
                return

Boundary fill algorithm (boundary-defined)

        Boundary-Fill(x,y, boundaryvalue, newvalue)
                if (get_pixel(x,y)  boundaryvalue AND
                        get_pixel(x,y)  new_value)
                        plotpoint(x,y, newvalue)
                        Boundary-Fill(x+1,y)
                        Boundary-Fill(x-1,y)
                        Boundary-Fill(x,y+1)
                        Boundary-Fill(x,y+1)
                return

Advantages of Seed fill algorithms:

1) don't have to have a mathematical description of the region - can be hand-drawn, or intersection of complex shapes

2) Simple algorithm

Disadvantages of Seed fill algorithms:

1) use lots of memory and are slow.

2) May miss regions of polygons because of narrow areas

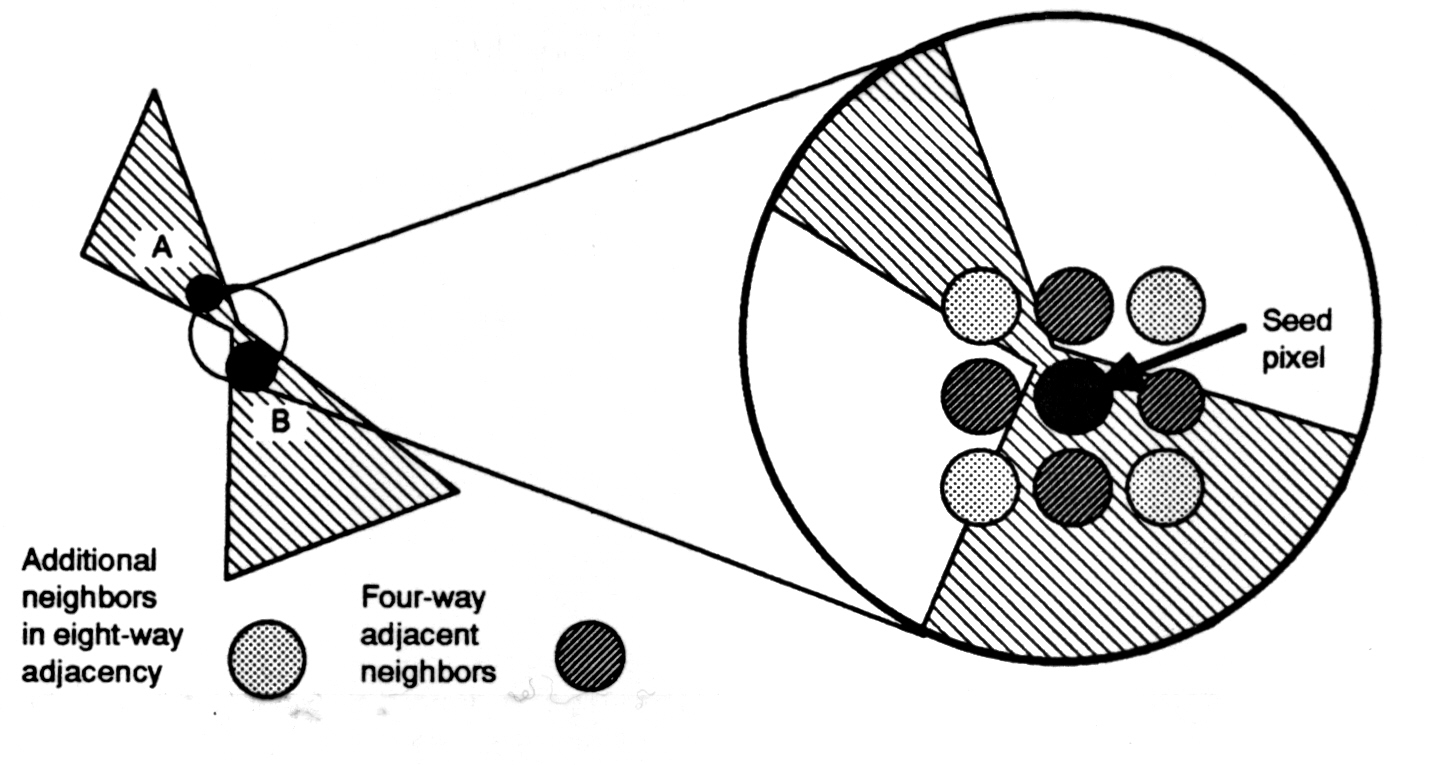
2) Scanline Seed Fill Algorithm

Has advantages of both the Scanline algorithm and the seed fill algorithms.
Pass a seed to the scanline fill algorithm.
Instead of checking neighbors recursively, it finds the longest sequence of pixels in the scanline that can be filled - the span of pixels (or run of pixels).
The left endpoint of the span is pushed onto the stack.
Loop Until Stack Empty

Pop off the top element on the stack

Find it's right end

Check the scanline above this span for any spans and push them on the stack.

Check the scanline below for any spans & push them on the stack

Draw line from left end to right end of current span.

End Loop

So the algorithm won't suffer from the large recursive stack needed for the seed fill algorithm.
Examples:

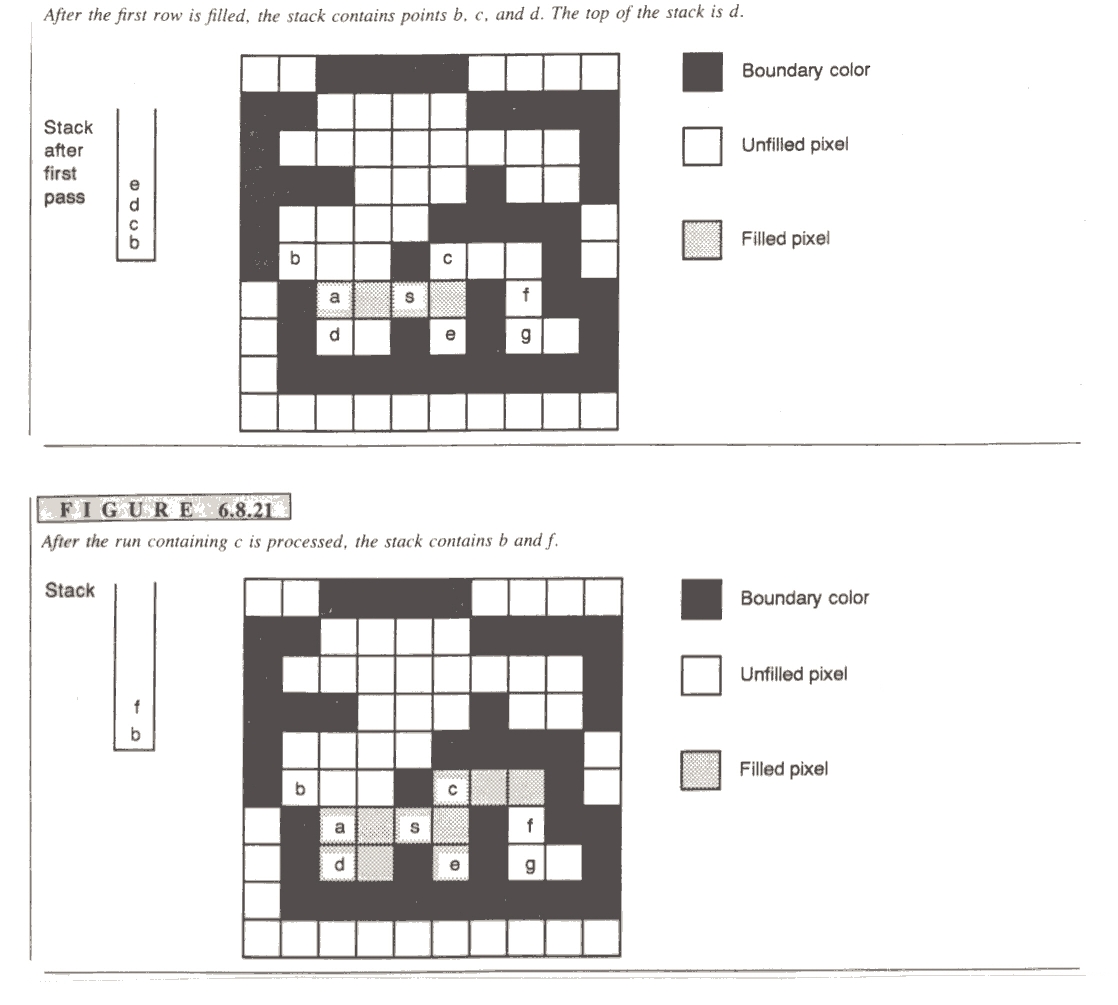
Example Code:

Example Code Here

3) Scanline Fill Algorithm

Intersect scanline with polygon edges.
Fill between pairs of intersections
Basic Structure

For y=ymin to ymax

1) intersect scanline with each edge

2) sort intersections by increasing x

3) fill pairwise (int0->int1, int2->int3, ...)

This is the basic structure, but we are going to handle some special cases to make sure it works right.
Also, will want to improve the speed by taking advantage of coherence:

the degree to which parts of an environment or its projection exhibit local similarities

span coherence- values don't change much from pixel to pixel in a span

scanline coherence - values don't change much from

one scanline to the next - the coverage (or visibility) of a face on one scanline typically differs little from the previous one.

edge coherence - edges intersected by scanline i are

typically intersected by scanline i+1

Geometry review:

Concave polygon: at least 1 interior angle > 180 degree

Convex polygon: all interior angles <= 180 degree

Filling the span from inti to intj

a) Fill from ceiling(inti) to floor(intj)

This gives us pixels that are interior to the polygon
Important when have polygons conntect to form an object (especially if each face has a different color)

b) Intersection has an integer x coordinate

If inti has an integer x coordinate, we define it to be interior
If intj has an integer x coordinate, we define it to be exterior

c) Intersection has an integer y coordinate

If this point is the ymin of the edge's endpoints, count it.
If the edge is horizontal and on the scanline, don't count it.

Examples :

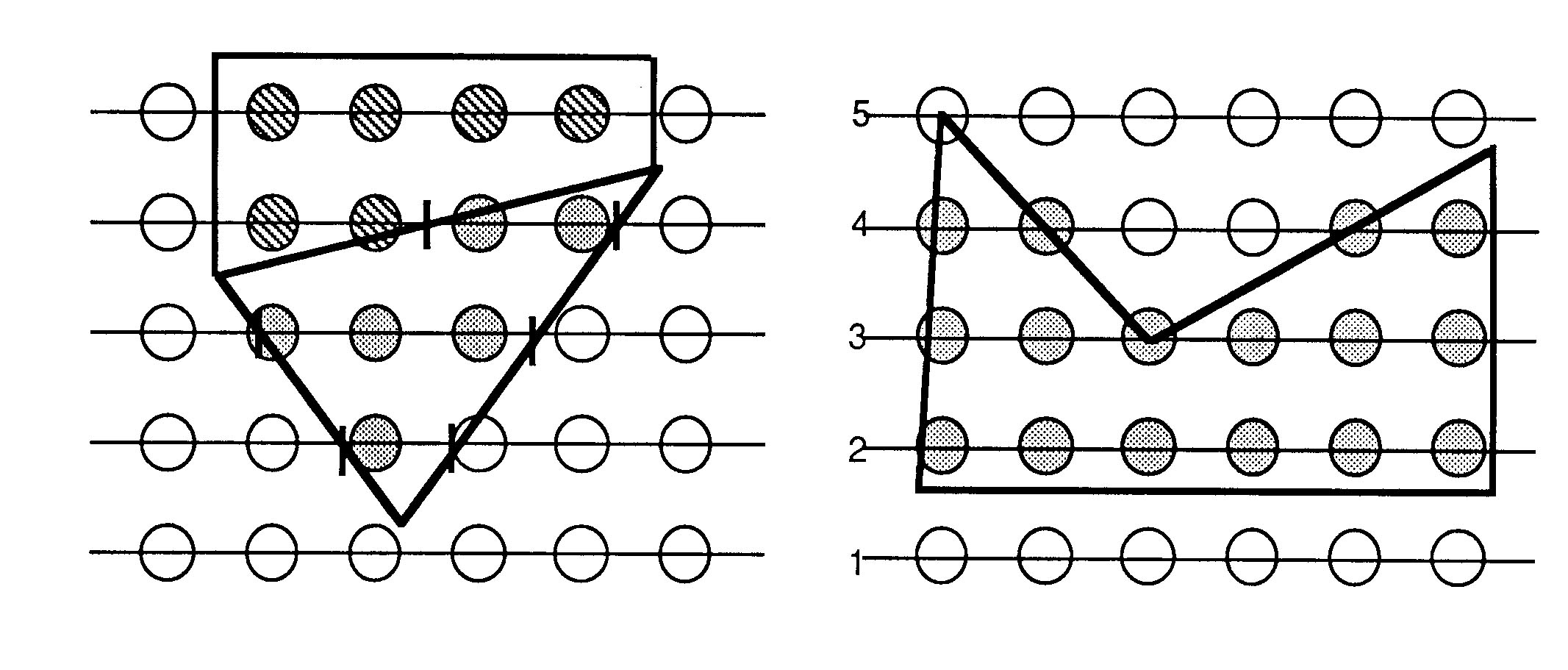
Intersctions with the scanline

Simple way is to just re-intersect all the edges with each scanline.

Improvement 1:

find the ymin & ymax of each edge & intersect it only if it crosses the scanline.

Improvement 2:

Only calculate the intersection of the edge with the first scanline it intersects.
Also calculate dx/dy.
For each additional scanline, calculate the new endpoint as x=x+dx/dy

Improvement 3:

change the x=x+dx/dy to integer arithmetic
suitable for simple polygon filling, but not really worth it in a scanline renderer or scanline Z-buffer renderer.

Data structures used in the algorithm:

Edge table: all edges sorted by their ymin coordinate. have a separate y bucket for each scanline. Within each bucket, edges sorted by increasing x of ymin point.

Edge structure: (ymax, xymin, dx/dy, pointer to next edge)

Active Edge Table: A list of edges that are active for this scanline, sorted by increasing x intersections.

Example Data structure Images

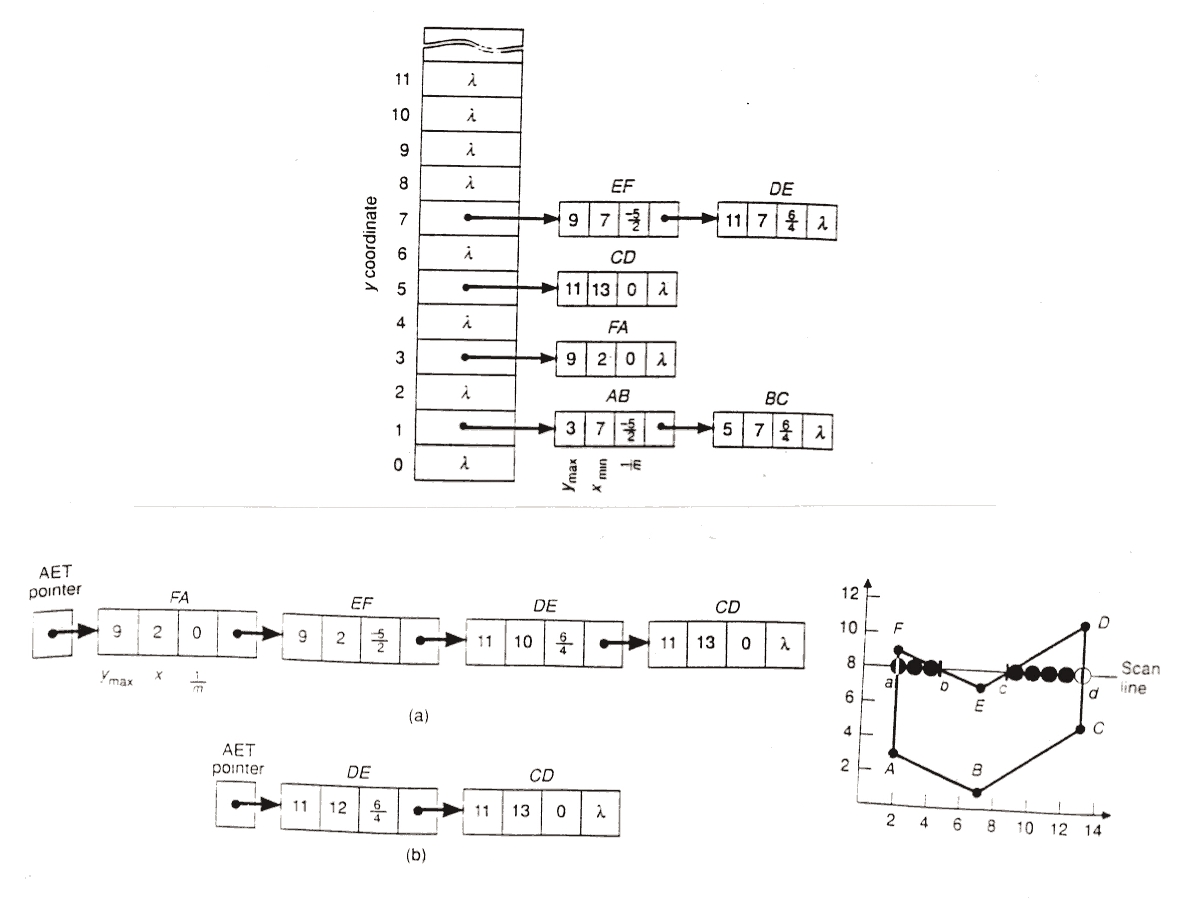
The algorithm:

scan-fill(polygon)

Construct the Edge table (ET)

        y = smallest y in the ET

        AET= null

        for y = ymin  to ymax
                Merge-sort ET[y] into AET by x value
                Fill between pairs of x in AET.
                for each edge in AET
                        if edge.ymax = y
                                remove edge from AET
                        else
                                edge.x = edge.x + dx/dy
                sort AET by x value
    end scan_fill