LINE CLIPPING

Want to clip lines to the window

(xmin, ymin, xmax, ymax)

Some cases trivial:

1) Trivial Accept

xmin <= x0, x1 <= xmax &&

ymin <= y0, y1 <= ymax

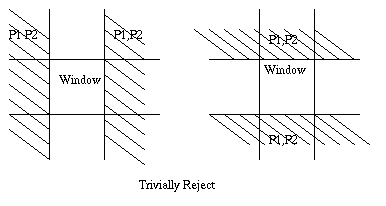
2) Trivial Reject :

x0, x1 <= xmin

y0, y1 <= ymin

x0, x1 >= xmax

y0, y1 >= ymax

Other cases:

1 inside window, 1 outside - intersect line with window and accept intersected line
Both outside (but not above cases) : Intersect with window, may or may not accept.

Line Clipping Algorithms:

1) Brute Force

2) Cohen-Sutherland

3) Liang-Barsky

4) Sutherland-Hodgman (closure clipping)

1) Brute Force

Use parametric equation of line:

x = x0 + t* (x1-x0)

y = y0 + t*(y1-y0)

Calculate intersection of line with window boundaries if not one of the trivial cases.
Have 4 unknowns and 4 equations, solve to get t and t_{window_edge}.
Example: Horizontal edge y =ymin:

y=y1 + t(y2-y1)=ymin

t=(ymin - y1)/(y2 -y1)

xint = x1 + (ymin -y1)/y2-y1) *(x2-x1)

make sure that 0<=t<=1 and

xmin<=xint<=xmax

Computationally very expensive

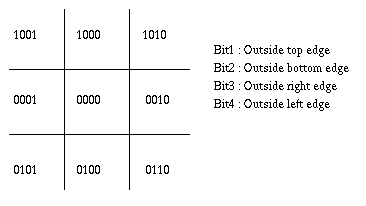
2) Cohen-Sutherland Algorithm

Based on calculation of outcodes for each end point :

Calculation of outcodes:

Bit1: y> ymax or sign(ymax-y)

Bit2: y < ymin or sign(ymin -y)

Bit3: x > xmax or sign(xmax -x)

Bit4: x < xmin or sign(xmin -x)

If (outcode(pnt1) OR outcode(pnt2))=0, then

trivially accept (logical OR -> all zeros)

if (outcode(pnt1) AND outcode(pnt2)) =1,

then trivially reject (if any bitwise and =1, then both point on same halfplane)

Else,

intersect line with a clip boundary and either trivially accept or reject one (or both) of the two parts.

Which clip edge do we intersect it with?

Well, if a outcode bit is 1, and we didn't reject the line, the line must cross that boundary.

Processing order is top, bottom, right, left.

So, The algorithm is essentially:

Calculate outcode(p1), outcode(p2)
Loop

Test for trivial rejection, acceptance. If so, exit loop
Else, choose one of the points that lies outside, call it P1 and see which boundary it crosses.
Intersect P1, P2 with the clip edge to get Pcl.
Through away (P1, Pcl), keep (Pcl, P2).
Compute outcode for Pcl.

end loop

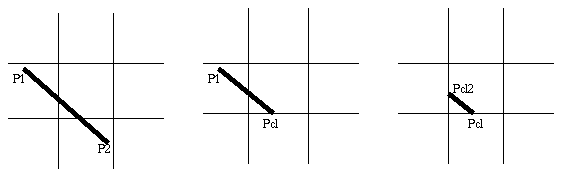
Example: P1: 0001 P2: 0100

can't trivially accept or reject, so clip against an edge
outcode[0] OK
Outcode[1] P2 outside, clip and keep P1,Pcl
calculate outcode(Pcl)= [0 0 0 0],
test Outcode[3], OK
Outcode[4], P1 outside c=> clip. keep Pcl, Pcl2.
Outcode(Pcl2)=[0 0 0 0], so draw (Pcl, Pcl2)

The final Cohen-Sutherland Clipping Algorithm

define TOP=1, BOTTOM=2, RIGHT=3 , LEFT=4

  CS-Clip(x0,y0, x1,y1)
     calc_code(x0, y0, outcode0)
     calc_code(x1, y1, outcode1)
     loop forever
        if (outcode0 = outcode1 = [0 0 0 0])
                drawline(p0,p1)
                return
        if (outcode0 & outcode1 != [0 0 0 0])
                return  /* trivial reject */
        if outcode0 = [0 0 0 0]  
                /* which one is outside */
                code= outcode1
                calc_intersect(code, x0, x1, 
                        y0, y1, x, y)
                x1=x, y1=y
                calc_code(x1,y1, outcode1)
        else 
                code = outcode0
                calc_intersect(code, x0, x1, y0, y1)
                x0=x, y0=y
                calc_code(x0,y0, outcode0)
      end loop

calc_intersect(code, x0,x1,y0,y1, x,y)
        if (code[TOP]) /* intersect top */
                x = x0 + (x1-x0)*(ymax - y0)/(y1-y0)
                y=ymax
        else if (code[BOTTOM])
                x = x0 + (x1-x0)*(ymin - y0)/(y1-y0)
                y=ymin
        else if(code[RIGHT])
                x=xmax
                y= y0 + (y1-y0)*(xmax - x0)/(x1-x0)
        else if(code[LEFT])
                x=xmin
                y= y0 + (y1-y0)*(xmin - x0)/(x1-x0)

3) Liang-Barsky Algorithm

Based on the parametric representation of the line:

x = x0 + t*(x1-x0)

y = y0 + t* (y1-y0)

Want the following restrictions on the solution:

        1)      x >= xmin       xmin <= x0 + t (x1-x0)
        2)      x <= xmax       xmax >= x0 + t (x1-x0)
        3)      y >= ymin       ymin <= y0 + t (y1-y0)
        4)      y <= ymax       ymax >= y0 + t (y1-y0)
        5)      0 <= t <= 1

Now, lets put all of these in the form t*m <= c

      1) t*( x0-x1)<= x0 -xmin      t*(-dx)
      2) t* (x1-x0)<= xmax - x0     t*dx
      3) t*(y0-y1)<= y0 -ymin       t*(-dy)
      4) t* (y1-y0)<= ymax - y0     t*(dy)

Range of t that satisfies these 5 inequalities is exactly where the line is visible.
So, we find T_min and T_max such that T_min <= t <= T_maxand we have our endpoints for visible portion of the line.
How do we use the above equations to find T_min & T_max?
First, set T_min =0, T_max = 1.
Now, we use the above inequalities to adjust T_min and T_max.
Remember,

1) t*(x0-x1) <= x0-xmin

2) t* (x1-x0) <= xmax - x0

3) t*(y0-y1) <= y0 -ymin

4) t* (y1-y0) <= ymax - y0

For each inequality (t*m <=c), calculate m & c:

If m > 0 then t <= c/m

Case 1: c/m < T_min, so the line is invisible

Case 2: c/m > T_max , doesn't change the range of t ( t < something bigger than Tmax , but t is < Tmax anyway.)

Case 3: T_min <= c/m² T_max, so set T_max = c/m

If m < 0 then t >= c/m

Case 1: c/m > T_max, so the line is invisible

Case 2: c/m <= T_min , doesn't change the range of t ( t >= something less than Tmin , but t is < Tmin anyway.)

Case 3: T_min <= c/m <= T_max, so set Tmin = c/m

If m=0, line is parallel to this clipping edge, so if c < 0, reject the line, otherwise do nothing.

If you didn't determine that the line was invisible, stick T_min and T_max in for t in the equations to get the endpoints for the visible portion of the line and draw it.
The Algorithm:

L-B_Clip(x0,y0,x1,y1, xmin, xmax, ymin, ymax)

   Tmin =0; Tmax=1
   dx = x1-x0; 

   if ( (RangeTest(-dx, x0-xmin,Tmin, Tmax)) == false)
        return;
   if ( (RangeTest(dx, xmax-x0,tmin, tmax)) == false)
        return;
   dy =y1-y0
   if ( (RangeTest(-dy, y0-ymin,Tmin, Tmax)) == false)
        return;
   if ( (RangeTest(dy, ymax-y0,Tmin, Tmax)) == false)
        return;

        /* line visible */
   if (Tmax  1)
        x1 = round(x0 + Tmax *dx)
        y1 = round(y0 + Tmax*dy)
   if (Tmin  0)
        x0 = round(x0 + Tmin *dx)
        y0 = round(y0 + Tmin*dy)
      drawline(x0,y0, x1,y1)
end L-B_Clip


        Boolean RangeTest(m,c, Tmin,Tmax)
                if(m >0)
                        r=c/m
                        if(r< Tmin)
                                return(false)
                        if( r < Tmax)
                                Tmax=r
                        return(true)
                if (m< 0)
                        r=c/m
                        if(r > Tmax)
                                return(false)
                        if( r > Tmin)
                                Tmin=r
                        return(true)
                if( c < 0)
                        return(false)
                return(true)
        end RangeTest

Example: Line from (1,1) to (9,6), Clip boundary (2,3) to (8,7)

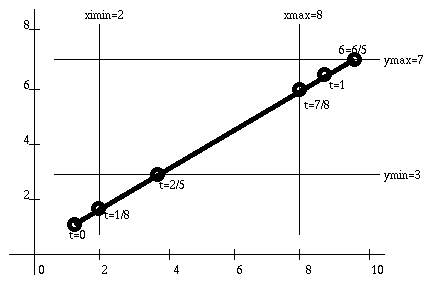
RangeTest1 sets Tmin=1/8,

RangeTest2 sets Tmax=7/8

RangeTest3 sets Tmin=2/5

RangeTest4 calculates r=6/5, but changes nothing

4) Sutherland-Hodgman

This algorithm clips a polygon into polygons. (the previous ones, clip lines to lines)
The approach is to clip the polygon to each of the infinite clipping edges in succession.

Cohen-Sutherland only clips a line against a boundary if necessary.
Assume we have a triangle of 3 line segments. Sutherland Hodgman clips the 3lines against 1 clip boundary, then the results against the next clip boundary,... . The result is always closed polygons
Cohen-Sutherland would clip line 1 against the clip boundaries (if necessary), then clip line2, then line3. The result will probably not be a closed a polygon.

Clip (vn, v0) ,(v0, v1), (v1, v2),....(vn-1,vn) against boundary1. Then the results against boundary2, etc.
Given the edge (s,p), where s's visibility has been handled before, there are 4 cases:

1) s in, p in => output p

2) s in, p out => output intersection

3) s out, p out => output nothing

4) s out,p in => output intersection, p

The generic algorithm takes an input vertex array and outputs the vertex array clipped to one edge.

For window clipping, make the inside routine test for inside of the 4 window edges, and call the clipper for each edge.

        Clip(InVert, OutVert, inlength, outlength, 
                clipedges)
                for i=0 to 3
                SH_CLIP(InVert, OutVert, inlength, 
                        outlength, i, clipedges)
                InVert=Outvert
                inlength=outlength
        end clip

Diagram

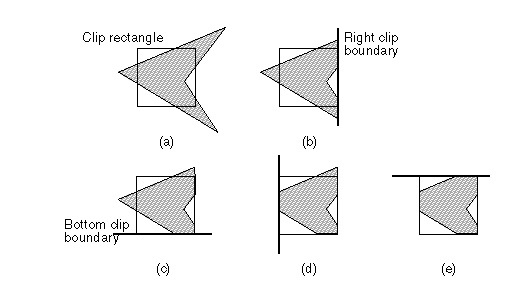
Algorithm to clip to 1 boundary

    SH_CLIP(InVert, OutVert, inlength, outlength,
                clipboundary, clip)
        outlength=0
        s = InVert[inlength -1]
        for (j=0 to inlength -1)
            p = InVert[j]
            if( Inside(p, clipboundary, clip)) 
                        /* case 1 &4 */
               if (Inside(s, clipboundary, 
                        clip)  /* case 1*/
                  output(p, outlength, OutVert)
                else  /* case 4*/
                   Intersect(s,p, clipboundary, clip, i)
                   output(i, outlength, OutVert)
                   output( p, outlength, OutVert)
            else /* case 2 & 3 */
                if(Inside(s, Clipboundary, clip)) 
                        /* case 2 */
                   Intersect(s,p, clipboundary,clip, i)                                                 
                output(i, outlength, OutVert)
          s=p
        end for
    end         

    boolean Inside(p, clipboundary, clip)
          case clipboundary of
                top:    return( p.y <= clip.top)
                bottom: return( p.y >= clip.bottom)
                left:   return( p.x >= clip.left)
                right:  return( p.x <= clip.right)
        end