LINE DRAWING

Description:

Given the specification for a straight line, find the collection of addressable pixels which most closely approximates this line.

Goals: (not all of them are achievable with the discrete

space of a raster device)

Straight lines should appear straight.
Lines should start and end accurately, matching endpoints with connecting lines.
Lines should have constant brightness.
Lines should be drawn as rapidly as possible.

Problem: How do we determine which pixels to illuminate to satisfy the above goals?

Vertical, horizontal, and lines with slope = +/- 1 easy.
Others create problems - staircasing/ jaggies - aliasing

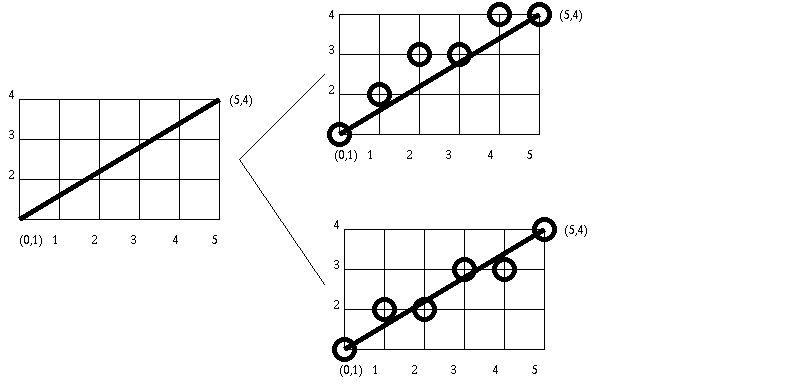
What we are going to look at are algorithms to choose which pixels to illuminate.

SOLUTION METHODS

1) Direct Solution:

Solve y=mx+b where (0,b) is the y-intercept and m is the slope.

Go from x0 to x1 calculate round(y) from the equation.

In the above example, b=1 and m = 3/5.

          If     x=1, y= 2
                 x=2, y= 2
                 x=3, y= 3
                 x=4, y= 3
                 x=5, y= 4.0

Why not use this?

* and / are expensive
round function needed
Can get gaps in the line (if slope > 1)

Example:

y=10x+2

x=1, y=12

x=2, y=22

2) DDA - Digital Difference Analyzer

Incremental Algorithm.

Based on y = (y1-y0)/(x1-x0) x + b

Assume x1 > x0 and |dx| > |dy| (can be easily modified for the other cases.)

The Algorithm:

        dx = x1-x0
        dy = y1 -y0
        m = dy/dx
        y=y0
        for (x=x0 to x1)
            draw_point (x, round(y))
            y=y+m
        end for

Problems:

Still uses floating point and round() inside the loop.

How can we get rid of these?

MIDPOINT LINE ALGORITHM

Incremental Algorithm
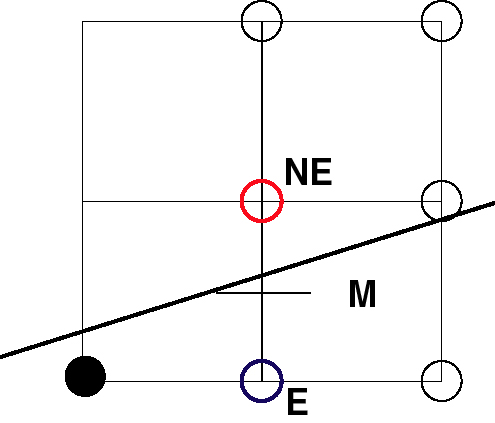
Given the choice of the current pixel, which one do we choose next (Assume first octant)
E or NE?

Equations:

y = dy/dx x + B
F(x,y) = ax +by +c =0

Gives: F(x,y) = dy*x - dx *y + B*dx =0

==> a=dy, b= -dx, c=B*dx

F(x,y) >0 if point below the line

F(x,y) < 0 if point above the line

Midpoint criteria:

d = F(M) = F(x_p+1, y_p+1/2)

if d >0 choose NE

d<= 0 choose E

Case EAST :

increment M by 1 in x

d_new= F(M_new) = F(x_p+2, y_p+1/2)

deltaE = d_new - d_old = a = dy

deltaE = dy

Case NORTHEAST:

increment M by 1 in both x and y

d_new= F(M_new) = F(x_p+2, y_p+1 1/2)

deltaNE = d_new - d_old = a + b = dy - dx

deltaNE = dy -dx

What is d_start?

d_start= F(x0+1, y0+ 1/2)

= ax0 +a + by0 + 1/2b + c

= F(x0, y0) + a + 1/2b = dy - 1/2dx

Let's get rid of the fraction and see what we end up with for all the variables:

d_start= 2dy -dx

deltaE = 2dy

deltaNE = 2(dy -dx)

So what is the algorithm?

The Midpoint Line Algorithm

        x       = x0
        y       = y0
        dy      = y1-y0
        dx      = x1 -x0
        d       = 2dy -dx
        deltaE = 2dy
        deltaNE = 2(dy -dx)

        PlotPoint(x,y)

        while (x <= x1)

          if d <=0    /* Choose E */
            d = d +deltaE
          else        /* Choose NE */
            d = d+ deltaNE
            y = y+1

          x = x+1
          PlotPoint(x,y)

        end while

How do you generalize this to the other octants?

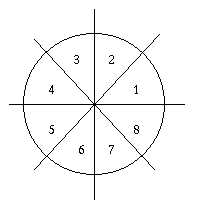
Octant                  Change

        1               none

        2               Switch roles of x & y

        3               ________________

        4               ________________

        5               Draw from P1 to P0

        6               ________________

        7               ________________

        8               Use y = y -1

Draw from P1 to P0: swap(P0,P1)

Use y =y -1: dy = -dy, y=y - 1

Switch X & Y:

Swap (x1, y1), Swap (x0, y0 ), Swap (dx, dy)

plotpoint(y,x)

CIRCLE DRAWING

Only considers circles centered at the origin with integer radii. Can apply translations to get non-origin centered circles.

Explicit equation: y = +/- sqrt(R2 - x2)

Implicit equation: F(x,y)= x2 + y2 - R2 =0

Note:

Implicit equations used extensively for advanced modeling (e.g., liquid metal creature from "Terminator 2")

Use of Symmetry: Only need to calculate one octant, can get points in the other 7 as follows:

        Draw_circle(x,y)
                Plotpoint (x,y)
                Plotpoint (x,-y)
                Plotpoint (-x,y)
                Plotpoint (-x, -y)
                Plotpoint (y,x)
                Plotpoint (y, -x)
                Plotpoint (-y, x)
                Plotpoint ( -y, -x)

Algorithms:

Direct Solution -

draw 2nd octant by incrementing x from 0 to R/sqrt(2)
at each step solve y = + sqrt(r2 - x2)

Midpoint Algorithm -

Just like before, we will find if the midpoint is above or below the curve.

MIDPOINT CIRCLE ALGORITHM

Will calculate for the second octant.
Use above procedure to calculate the rest.

Now will choose between pixel S and SE.

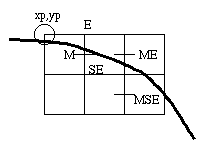
F(x,y) = x2 + y2 - R2 =0

F(x,y) >0 if point is outside circle

F(x,y) <0 if point inside circle.

Again, use d_old=F(M)

F(M) = F(x_p+1, y_p-1/2) = (x_p +1)² + (y_p -1/2)²- R²

d >= 0 choose SE

next midpoint = M_new + 1 in X, -1 in y= d_new

d <0 choose E

next midpoint = M_new + 1 in X = d_new

deltaE = d_new - d_old =

F(x_p+2, y_p-1/2) - F(x_p+1, y_p-1/2)

deltaE = 2x_p +3
deltaSE = F(x_p+2, y_p - 3/2) - F(x_p +1, y_p -1/2)

deltaSE = 2x_p - 2y_p + 5

d_start = F(x0+1, y0 -1/2) = F(1, R-1/2)

= 1 + (R -1/2)2 - R2 = 1 + R2 -R + 1/4 - R2

= 5/4 - R

To get rid of the fraction, lets let h = d - 1/4 => hstart = 1 -R

Comparison is h < -1/4,

but h initialized to & incremented by

integers, so can just do h < 0

The Midpoint Circle algorithm: (Version 1)

        x=0
        y=R
        h = 1 - R
        DrawCircle(x,y)
        while (y > x)
           if h < 0         /* select E */
               h = h + 2x + 3
           else             /* select SE *
               h =h + 2(x-y) +5
               y = y -1
           x = x +1
           DrawCircle(x,y)
        end_while

Problems with this?

Requires at least 1 multiply and 3 adds per pixel. Why? because deltaE and deltaSE are linear functions not constants.
Can we do better?

Sure we can.

All we have to do is calculate the differences for deltaE and deltaSE (these will be constants) : deltadeltaE and deltadeltaSE.

If we chose E, the we calculate deltadeltaE and deltadeltaSE based on this, same if we chose SE.

If we chose E, go from (x_p, y_p) to (x_p+1, y_p)

deltaE_old was 2x_p +3, deltaE_new is 2x_p +5

deltadeltaE = 2

deltaSE_old= 2x_p -2y_p +5,

deltaSE_new =2(x_p+1) -2y_p+5

deltadeltaSE = 2

If we chose SE, go from (x_p, y_p) to (x_p+1, y_p -1)

deltaE_oldwas 2x_p +3, deltaE_new is 2x_p +5

deltadeltaE = 2

deltaSE_old= 2x_p -2y_p +5,

deltaSE_new=2(x_p+1) -2(y_p-1)+5

deltadeltaSE = 4

So, at each step, we not only increment h, but we also increment deltaE and deltaSE.
What are deltaE_startand deltaSE_start ?

deltaE_start= 2*(0) +3 =3

deltaSE_start = 2*(0) -2*(R) +5

The MidPoint Circle Algorithm (Version 2):

        x=0
        y=radius
        h= 1 -R
        deltaE=3
        deltaSE=(-2 *R +5)
        DrawCircle(x,y)
        while (y > x)
           if h < 0      /* select E */
              h = h +deltaE
              deltaE= deltaE + 2
              deltaSE= deltaSE + 2 
           else         /* select SE */
              h = h + deltaSE
              deltaE= deltaE + 2
              deltaSE= deltaSE + 4
              y = y -1
           x = x+1
           DrawCircle(x,y)
         end_while