CMSC313, Computer Organization & Assembly Language Programming, Spring 2013
Homework 3
Due: Tuesday April 30, 2013
Paper submissions are due in class. Logisim circuits can be submitted
online up to 11:59pm of the due date using the submit command
on GL. Make a copy of your paper submission, if you need it to construct
your Logisim circuit.
Problem #1 (30 points)
Using the Basic Identities of Boolean Algebra in Table 3.5 (p. 125),
simplify the following formulas. Show all of your work and justify each
step.
-
( A + (C + B) ) ⋅ ( ~( ~B ⋅ ~C ) )
-
~( ~A ⋅ B ) ⋅ ~( ~A ⋅ ~B ) + A ⋅ C
Note: here + means OR, ⋅ means AND, and
~ means NOT.
Problem #2 (30 points)
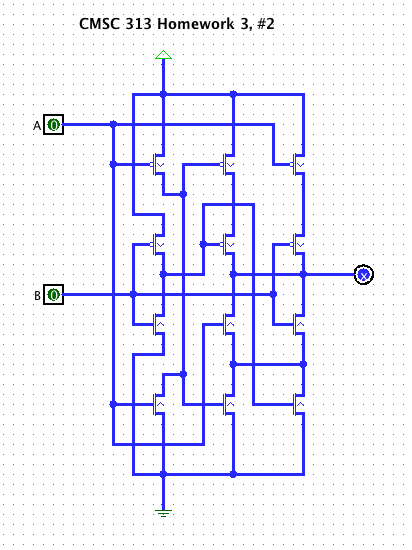
For the CMOS circuit shown below,
- (10 points)
Provide a truth table for the circuit's function. You may use the
Logisim circuit, hw3-2.circ, to determine
the truth table. (You must download the circuit on your machine and
run Logisim.)
- (5 points)
Write down the Sum-of-Products (SOP) Boolean formula for the truth table.
- (5 points)
Write down the Product-of-Sums (POS) Boolean formula for the truth table.
- (10 points)
Draw the logic diagram of the POS formula using AND, OR and NOT gates (do not simplify).
Problem #3 (40 points)
For this problem, you will build a 4-bit Arithmetic Logic Unit (ALU)
that adds, subtracts, decrements and increments in Logisim. The design is
based on the
Combined Adder/Subtractor shown in class:
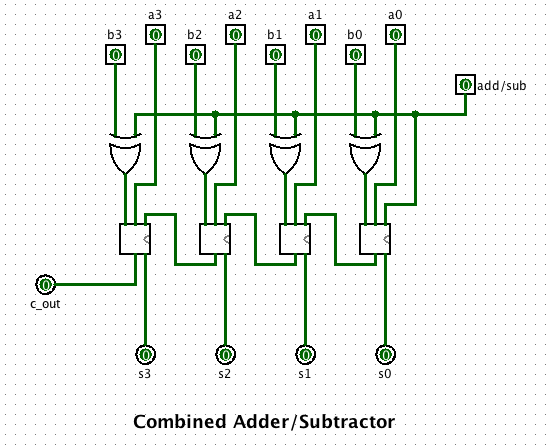
We can think of this circuit as having 1 control line that determines
whether the circuit adds or subtracts. Our 4-bit ALU will have two
control lines (d1 d0) that determines whether the ALU will add,
subtract, decrement or increment:
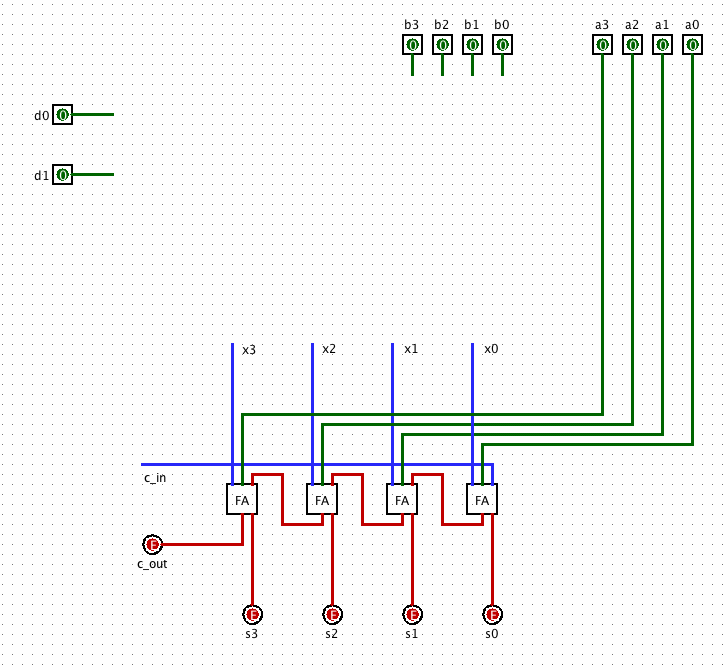
This functionality can be built using just the 4-bit ripple-carry
adder. Your problem is to figure out how to connect x3 x2 x1 x0 to
d1 d0 and b3 b2 b1 b0. Follow these steps:
First, we write down what we want to accomplish:
- d1 d0 = 00 (ADD)
We want to add b3 b2 b1 b0 to a3 a2 a1 a0 and provide the sum
in s3 s2 s1 s0. This can be accomplished by passing each b_i
unchanged thru to x_i.
- d1 d0 = 01 (SUB)
We want to subtract b3 b2 b1 b0 from a3 a2 a1 a0 and provide
the difference in s3 s2 s1 s0. We can use the same
trick that the Combined Adder/Subtractor used: make x_i the complement
of b_i and set the carry-in (c_in) to 1. That effectively
adds the two's complement of b3 b2 b1 b0 to a3 a2 a1 a0.
- d1 d0 = 10 (DEC)
We want to subtract 1 from a3 a2 a1 a0 and provide the result
in s3 s2 s1 s0. In this case, the values in b3 b2 b1 b0 are ignored.
We can subtract 1 by adding 1 1 1 1 to a3 a2 a1 a0, since 1111 is
−1 in 4-bit two's complement. Thus, each x_i should simply be
set to 1 in this case. The carry-in should be 0.
- d1 d0 = 11 (INC)
We want to add 1 to a3 a2 a1 a0 and provide the result in
s3 s2 s1 s0. As in the case for DEC, we ignore b3 b2 b1 b0.
To add 1, we simply set each x_i to 0 and make c_in 1.
From the description above, we can produce a truth table for the values
of x_i and c_in, given the inputs d1, d0 and b_i:
| d1 | d0 | bi | xi | c_in |
|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 |
What to do:
-
On a piece of paper to be turned in with Problems 1 and 2, write down a
Boolean formula for x_i in terms of d1 d0 and b_i. Simplify the formula
as much as you can. Clearly indicate your final formula for x_i.
-
Write down a formula for c_in. Simplify the formula as much as you
can. Clearly indicate your final formula for c_in.
-
Download the starting point for your circuit:
hw3-3.circ.
-
In Logisim, connect the ripple-carry adder's inputs, x3 x2 x1 x0, to d1 d0 and
b3 b2 b1 b0 according to your formula from the previous step.
(Yes, you will have four copies of the same circuit. You can
use copy-paste to do this more quickly.)
-
In Logisim, connect c_in to d1 d0 and b0 according to your formula
for c_in from above.
-
Test your ALU and make sure that it works as advertised.
-
Save your circuit diagram, transfer the file to GL and submit from
GL as usual:
submit cs313 hw3 hw3-3.circ
-
Submit the work done on paper in class along with
your work for Problems #1 & #2.
Implementation notes:
-
When you simplify your Boolean formula, you want to reduce the number
of gates. This might not correspond to a "simpler" formula as defined
in high school and middle school Algebra.
-
Give some thought to the layout of your circuit. Neatness will count in
grading.
-
Logisim gates come in three sizes: narrow, medium and wide. Pick the
appropriate size.
-
Logsim gates can have negated inputs (bubbles). This can greatly
simplify your circuit's layout because you do not need to make room
for NOT gates. To negate a particular input, select the gate using
the arrow tool. Then, in the panel on the lower left,
choose "Yes" to negate a particular input line.
Last Modified:
23 Apr 2013 07:17:24 EDT
by
Richard Chang
 to Spring 2013 CMSC 313 Homepage
to Spring 2013 CMSC 313 Homepage




 to Spring 2013 CMSC 313 Homepage
to Spring 2013 CMSC 313 Homepage