- G does not contain any cycles.
- e = n − 1.
- there is a unique path between every pair of vertices in G.
Proof:
(I ⇒ II)
Suppose that G does not contain any cycles. We first
argue that G must have a vertex with degree 1 as long
as G has at least 2 vertices. (We do this because when
we remove a degree 1 vertex, we do not disconnect the graph and
we reduce the number of vertices and edges by 1.) To see this,
we explore the graph along a path. We start at any vertex and
move along an edge to another vertex. We keep moving along edges
but we do not reuse the edge that we used to arrive at the current
vertex. If we revisit a vertex at any point, then we have
discovered a cycle. Since G does not have any cycles,
this is impossible. Thus, each vertex we visit must be a new vertex.
Since there are only n vertices in G, after at
most n steps we cannot discover any more new vertices.
That means, the last vertex, the one we stopped at, must have
degree 1. If there is an edge other than the one that we just
used to arrive at the last vertex, then that edge would either
lead to a previously visited vertex (creating a cycle) or to a
new vertex (which implies that G has more than n
vertices) — either of which leads to a contradiction.
Now, remove the degree 1 vertex we found from G. The
resulting graph is still a connected graph without any cycles,
which by the argument above, must have a degree 1 vertex. We
keep removing the degree 1 vertices until all we have is a single
vertex and no edges. Each time we removed a degree 1 vertex, we
reduce the number vertices by 1 and the number of edges by 1.
Let m be the number of degree 1 vertices we removed in
the process. Then, e must equal m and n
must equal m + 1, since the removal process took away all
of the edges and all but one of the vertices. Thus, e =
n − 1.
(II ⇒ III) We prove this indirectly. That is, we show
that ¬III ⇒ ¬II. In other words, we will show that if there are
two paths in G between some pair of vertices u and
v, then e ≠ n - 1. So, suppose that
there are two paths π1 and
π2 from u to v:
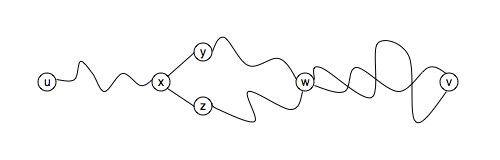
As before, we keep removing degree 1 vertices from G until there are no more degree 1 vertices. Now, we are not allowed to assume that G does not have any cycles, since in proving II ⇒ III we are not allowed to assume I. So, it might be the case that G does not have degree 1 vertices, but that's OK. This argument takes a different route. Suppose that m vertices are removed when we remove degree 1 vertices. (It is possible that m = 0.) Let G' be the resulting graph.
Consider the cycle from x to itself that we found above — the one going through y, w and z. None of the vertices in this cycle was removed. Why is this? Suppose some vertex a is the first vertex from the cycle to be removed. But, if a was first, then a was still connected to two vertices in the cycle. That means, a still had degree 2 and should not have been removed — a contradiction. Thus, the process of removing degree 1 vertices will leave at least 4 vertices in G'.
Let n' and e' be respectively the number of vertices and edges in G'. Every vertex in G' has degree at least 2, so we have:
and
2 e' = ∑ degree(v) v ∈ G'
We know summing the degrees always gives us twice the number of edges. That accounts for the first equation. The second comes from every vertex in G' having degree at least 2. Thus, 2 e' ≥ 2 n' which implies that e' ≥ n'. Finally, in terms of the number of vertices n and the number of edges e in the original graph G, we have e = e' + m and n = n' + m because m degree 1 vertices were removed from G to form G'. Thus,
∑ degree(v) ≥ 2 n'. v ∈ G'
e = e' + m ≥ n' + m = n.Therefore, e is at least n (thus cannot be equal to n − 1) and we have shown that ¬III ⇒ ¬II.
(III ⇒ I) We prove this indirectly and and show that if G has a cycle then the path between some pair of vertices u and v is not unique. So, suppose that G has a cycle x1, x2, x3, ..., xk, x1. Then, let u = x1 and v = x2. The edge between x1 and x2 constitutes a path from u to v. Furthermore, the reversal of the portion of the cycle from x2 to xk back to x1 is also a path from u to v. Thus, there are two paths in G from u to v.
 to Spring 2016 CMSC 203-06 Homepage
to Spring 2016 CMSC 203-06 Homepage