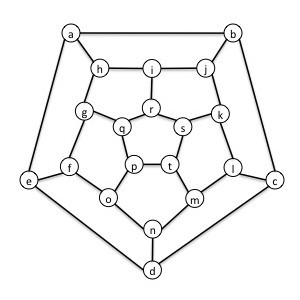
In the graph below, find a vertex cover with as few vertices as you can. List the vertices of the vertex cover you found and briefly argue that it is the smallest possible.
Hint: the smallest vertex cover in this graph has 10 vertices.
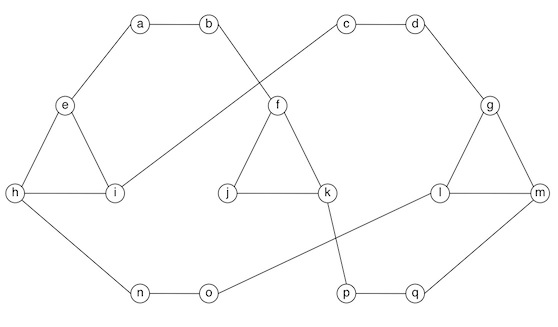
A graph has a Hamiltonian circuit if there is a path in the graph that visits every vertex exactly once and returns to the first vertex in the path.
- Does the graph below have a Hamiltonian circuit? Justify your answer.
- In general, if a graph has a Hamiltonian circuit, is it necessarily the case that the graph has an Euler circuit? Justify your answer.
- In general, if a graph has an Euler circuit, is it necessarily the case that the graph has a Hamiltonian circuit? Justify your answer.
- Draw a 3-regular graph with 6 vertices.
- Draw a 3-regular graph with 8 vertices.
- Draw a 3-regular graph with 10 vertices.
- Are there any 3-regular graphs with 9 vertices? why or why not?
 to Spring 2016 CMSC 203-06 Homepage
to Spring 2016 CMSC 203-06 Homepage