| ⇐ Proofs by Contradiction | Proof by Cases ⇒ |

Claim: There exists a triangle-free graph that is 4-colorable, but not 3-colorable.
Proof: Consider the following graph and its 4-coloring:By checking every triple of vertices, the reader can verify that the graph is triangle-free. We leave the proof that the graph is not 3-colorable as an exercise. 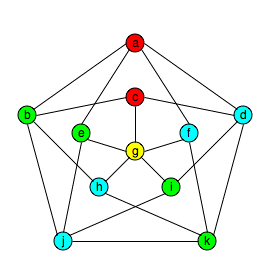 QED
QED
Claim: There exist irrational numbers x and y such that xy is rational.
Proof: Let z = √2 √2 . If z is rational then z is our desired number with x = √2 and y = √2.Now, suppose that z is irrational. Then, let x = z and y = √2.
xy = (√2 √2 ) √2 = √2 ( √2 ⋅ √2 ) = √2 2 = 2.In this case, xy is again rational.In either case, whether z is rational or irrational, we've shown the existence of irrational numbers x and y such that xy is rational.
QED
| ⇐ Proofs by Contradiction | Proof by Cases ⇒ |
 to Spring 2009 CMSC 203 Homepage
to Spring 2009 CMSC 203 Homepage