Claim:
For all x ≥ 0, ⌈ x/2 ⌉
≥ ⌈ x ⌉ /2 .
Proof:
We break up the proof into three cases:
- x is an even integer.
- x is an even integer plus some ε,
0 < ε < 1.
- x is an odd integer.
- x is an odd integer plus some ε,
0 < ε < 1.
Case 1: x = 2n for some integer n ≥ 0.
Then,
⌈ x/2 ⌉
= ⌈ 2n/2 ⌉
= ⌈ n ⌉
= n.
Also,
⌈ x ⌉/2
= ⌈ 2n ⌉/2
= 2n/2
= n.
Thus, ⌈ x/2 ⌉ ≥
⌈ x ⌉ /2 .
Case 2: x = 2n + ε for some integer
n ≥ 0 and some real number ε
where 0 < ε < 1.
Then,
⌈ x/2 ⌉
= ⌈ (2n + ε)/2 ⌉
= ⌈ n + ε/2 ⌉
= n + ⌈ ε/2 ⌉
= n + 1.
We know ⌈ ε/2 ⌉ = 1
because 0 < ε/2 < 1/2. Also,
⌈ x ⌉ /2
= ⌈ 2n + ε ⌉ /2
= (2n + ⌈ ε ⌉) /2
= (2n + 1) /2
= n + 1/2.
Again, we have ⌈ x/2 ⌉ ≥
⌈ x ⌉ /2 .
Case 3: x = 2n+1 for some integer n ≥ 0.
Then,
⌈ x/2 ⌉
= ⌈ (2n + 1)/2 ⌉
= ⌈ n + 1/2 ⌉
= n + ⌈ 1/2 ⌉
= n + 1.
Also,
⌈ x ⌉ /2
= ⌈ 2n + 1 ⌉ /2
= (2n + 1)/2 = n + 1/2.
Thus, ⌈ x/2 ⌉ ≥
⌈ x ⌉ /2 .
Case 4: x = 2n + 1 + ε
for some integer n ≥ 0 and
some real number ε where 0 ≤ ε < 1.
Then,
⌈ x/2 ⌉
= ⌈ (2n + 1 + ε)/2 ⌉
= ⌈ n + 1/2 + ε/2 ⌉
= n + ⌈ 1/2 + ε/2 ⌉
= n + 1.
We know ⌈ 1/2 + ε/2 ⌉ = 1
because ε < 1. Also,
⌈ x ⌉ /2
= ⌈ 2n + 1 + ε ⌉ /2
= (2n + 1 + ⌈ ε ⌉) /2
= (2n + 2) /2 = n + 1.
Thus, we have ⌈ x/2 ⌉ ≥
⌈ x ⌉ /2 in the final case.
QED
Claim: The graph K3,3 shown below is not
a planar graph.
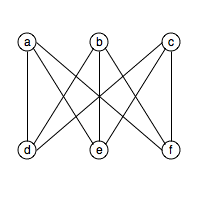
Proof: Consider the vertices a, f, c
and d. They form a cycle in the graph K3,3.
Any planar drawing K3,3 cannot have the edges
cross, so the cycle divides the plane into two regions: inside
and outside the cycle. Now, the vertex b can either be
placed inside or outside the a-f-c-d-a cycle:
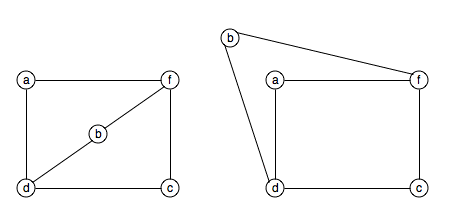
Case 1: Suppose that the vertex b is placed inside
the cycle. Now, consider where the vertex e can be placed.
There are 3 possible regions: inside the region bounded by
a-f-b-d-a, inside the region bounded by c-d-b-f-c
or outside the a-f-c-d-a cycle.
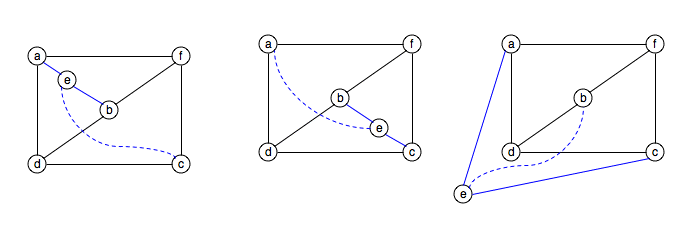
In each of these possibilities, there is an edge that cannot be drawn
without edges crossing.
Case 2: If the vertex b is place outside the
a-f-c-d-a cycle, we make the same argument about the
placement of vertex e, except the roles of vertices
a and b are interchanged.
QED



 to Spring 2008 CMSC 203 Section Homepage
to Spring 2008 CMSC 203 Section Homepage