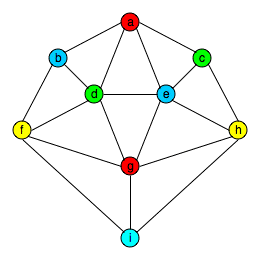
Proof: Here is a 4-coloring of the graph. We leave it to the reader to check that every pair of adjacent vertices (the vertices connected by an edge) are colored with different colors.
QED
| ⇐ Proofs & English | Indirect Proofs ⇒ |
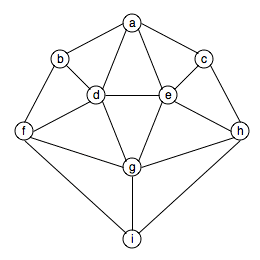
Example:
Claim: The graph below is 4-colorable.

Proof: Here is a 4-coloring of the graph. We leave it to the reader to check that every pair of adjacent vertices (the vertices connected by an edge) are colored with different colors.
 QED
QED
| ⇐ Proofs & English | Indirect Proofs ⇒ |
 to Spring 2008 CMSC 203 Section Homepage
to Spring 2008 CMSC 203 Section Homepage