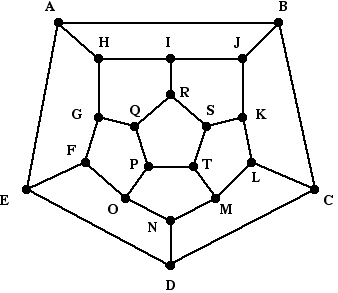
A graph has a Hamiltonian circuit if there is a circuit in the graph that visits every vertex exactly once. Does the graph below have a Hamiltonian circuit? Justify your answer.
A space traveler returns from the Betelgeuse star system and gives a report on the aliens encountered there:
It is not true that if the aliens are green then they either have three heads or else they cannot fly, unless it is also true that they are green if and only if they can fly and that they do not have three heads.Assume that the aliens are all alike. Let f be the proposition that "the aliens can fly", let g be the proposition that "the aliens are green" and let h be the proposition that "the aliens have three heads".
Use logic notation and the variables f, g and h to rephrase the space traveler's report.
Can the aliens fly? Are they green? Do they have 3 heads? Show your work.
 to Spring 2008 CMSC 203 Section Homepage
to Spring 2008 CMSC 203 Section Homepage