A proof by contradiction is similar to an indirect proof. However,
indirect proofs are used with implications, whereas, a proof by
contradiction can be used in a more general setting.
Claim: There are an infinite number of prime numbers.
Proof: Suppose not. Then, there is a finite number of
prime numbers and we can let p1,
p2, ..., pn be all
the prime numbers. We define
Q = p1 p2 ...
pn + 1.
If Q is prime, then Q is a prime number not on
the list p1, p2, ...,
pn because Q is larger than
every pi. That contradicts the assumption that
p1, ..., pn contain all of
the prime numbers.
On the other hand, suppose that Q is composite. Let
q be a prime factor of Q. Note that Q is
not divisible by any of the pi. Why? because
the product p1 p2 ...
pn is a multiple of pi and
the next multiple of pi is p1
p2 ... pn + pi.
Since
p1 p2 ... pn
< Q <
p1 p2 ... pn
+ pi,
Q cannot be a multiple of pi. That
means the prime factor q of Q does not appear
on the list of prime numbers p1,
p2, ... pn since Q
is a multiple of q. Thus, we also have a contradiction
in this case.
In either case, we found a prime number not on the list of prime
numbers. Thus, we can conclude that our premise that there is a finite
number of prime numbers must be false. Thus, there must be an infinite
number of primes.
QED
Claim: The graph below is not 3-colorable.
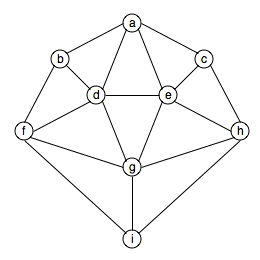
Proof: Suppose by contradiction that the graph is
3-colorable using 3 colors we'll call red, green and blue. Then,
every vertex in the graph is colored red, green or blue. Without
loss of generality, let the color of vertex a be red.
Vertices b and d must be colored different colors
that are not red. Let these two colors be, respectively, blue
and green. Now, vertex e is adjacent to vertices a
and d, so it cannot be colored red or green. Thus, vertex
e must be colored blue. Similarly, c must be green,
g must be red and we arrive at the following partial
coloring:
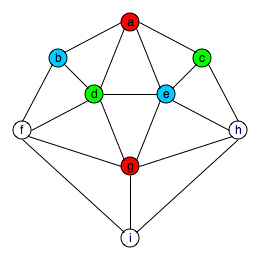
Note that vertex f is adjacent to vertices b,
d and g, which are, respectively, blue, green and
red. Thus, vertex f cannot be colored blue, green or red.
This contradicts our previous conclusion that every vertex is
colored red, green or blue. Thus, our initial assumption that
the graph is 3-colorable must be false.
QED


 to Fall 2010 CMSC 203 Homepage
to Fall 2010 CMSC 203 Homepage