UMBC CMSC202, Computer Science II, Fall 1998,
Sections 0101, 0102, 0103, 0104
24. Expression Trees
Tuesday December 01, 1998
[Previous Lecture]
[Next Lecture]
Assigned Reading: none
Handouts (available on-line):
Programs from this lecture:
Topics Covered:
- Discussed the extra credit portion of
Project 5. Some highlights:
- Suppose that we have a Binary Search Tree (BST) that satisfies the
condition that at every subtree with 5 or more nodes, neither subtree is
more than twice the size of the other subtree. We argued that the height of
such a BST is O(log n). In fact, it is roughly log(3/2) n.
- Since the height of such a balanced tree is O(log n), BST operations
such as find and max take O(log n) time.
- Insert and delete might take O(n) time in the worst case, since we may
have to rebalance the tree during an insertion or a deletion.
- However, not every insert and delete would require us to rebalance the
tree. We argued (not very rigorously) that on average the running time of
insert and delete is also O(log n). This average is taken over the
operations performed on the BST (we are not taking the average over the
data stored in the tree). In such a situation, we say that the
amortized running times of insert and delete are O(log n).
- Another kind of binary tree is an expression tree --- a
representation of arithmetic expressions. For example, the expression
2 + 3 can be represented as a binary tree with a root labeled with +.
The root would have two children labeled with 2 and 3. For more
complicated arithmetic expressions, the root of the tree is the
operation that is performed last. The left subtree and right subtree
of the root are the left and right operands of that last operation.
For example, in the expression (2 + 3) * (4 + 5), the * is performed
last, so the left and right subtrees represent (2 + 3) and (4 + 5),
respectively.
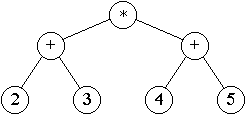
Note that in an expression tree, we do not need to store parentheses,
since the order of evaluation is implicit in the structure of the
tree.
- We can use the template Tree class from Lecture 22 to instantiate an
expression tree class. Each node of the expression tree will be an object
from a Token class which we describe below. We use the expression tree to
help us build a calculator program. This program considers operator
precedence of * over + and works with nested parentheses. Another feature
of this program is its ability to report errors (and point to the location
of the syntax error). See sample run.
- The calculator program is divided into 2 parts. The parser (header file and implementation) works with higher level
concepts (expressions, terms and factors). The tokenizer (header file and implementation) does the string and character
manipulations for the parser. The TokenStream class is initialized
with a string which contains an arithmetic expression. The member
functions look() and eat() allows us to obtain the
next syntactic unit of the string (the next number, operator, etc.).
This syntactic unit is returned as an object of type Token.
- The parser essentially follows the derivation rules for a legal
arithmetic expression. The grammar we use to describe the set
of allowed expressions is:
Expression -> Term + Expression
Expression -> Term - Expression
Expression -> Term
Term -> Factor * Term
Term -> Factor / Term
Term -> Factor
Factor -> ( Expression )
Factor -> Number
- We showed how a simple expression like (3 + 4) * (72 - 70) can be
derived using the grammar above. This is a mechanical process that is
tedious to do by hand, but perfect for a program to follow.
- Our parser is simply a set of
mutually recursive functions (ParseExpression(), ParseTerm()
and ParseFactor()) that follow the rules for deriving these
arithmetic expressions. If any of these functions find an error, it throws
an exception. Each of these functions also catches exceptions.
When an exception is caught, memory for any partially built expression
trees is deallocated. Then the exception is rethrown to be
caught again and rethrown again ... until the function Parse()
finally catches the exceptions for the last time.
- The function evaluate() recursively computes the value of
an expression tree. Thus, we have all the parts of a calculator
program. Build an expression tree from an arithmetic expression and
use evaluate() to determine the value of the expression.
[Previous Lecture]
[Next Lecture]
Last Modified:
4 Dec 1998 23:02:40 EST
by
Richard Chang
Back up
to Fall 1998 CMSC 202 Section Homepage
