CMSC 341 - Fall 1998 -- Final Exam Review

1. Define "Big-Oh"
2. Number these functions in ascending "Big-Oh" order
O(n²), O(n lg n), O(1), O(lg^0.1 n), O(2ⁿ), O (lg n), O(sqrt(n))
3. Prove O(cf(x)) = O(f(x))
4. Suppose T₁(n) = O(f(n)) and T₂(n) = O(f(n)).Prove that T₁(n) + T₂(n) = O(f(n))
5. Define the following

11. Prove that in any undirected graph, |E| = O(|V|²)
12. Write pseudo-code for breadth-first and depth-first traversals of undirected graphs. The code must be complete and fully describe the operations.
13. Let G = (V, E) be an undirected graph with V the set of vertices and E the set of edges. Let v₁, v₂, . . . V_p be all the members of V and let q = |E|, the cardinality of E. Prove that the sum of the degrees of all vertices = 2q.
14. Describe any adjacency table implementation for a graph. How does it differ for directed and undirected graphs?
15. Describe any adjacency list implementation for a graph. How does it differ for directed and undirected graphs?
16. Briefly describe the adjacency table and adjacency list implementations of a graph -- include advantages and disadvantages; describe the asymptotic worst-case storage requirements for each and describe the worst-case asymptotic performance of the operations below. Note that u and v are vertices in the graph.

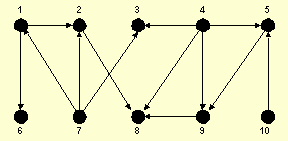
17. Find a topological sorting for the given directed graph. Describe the method you used and show all your work.

    

18. Describe Prim's algorithm for generating a minimum-spanning tree in a weighted undirected graph. What is the "Big-Oh" performance of Prim's algorithm? Justify your answer.
19. Describe Kruskal's algorithm for generating a minimum-spanning tree in a weighted, undirected graph. What is the Big-Oh performance of Kruskal's algorithm? Justify your answer.
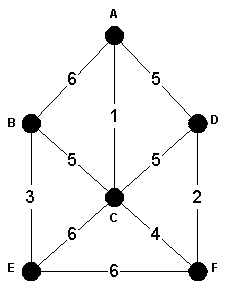
20. Find the minimum-spanning tree for the given weighted-undirected graph below using both Prim's and Kruskal's algorithm. Show your work.
    

21. Define the single-source shortest path problem.
22. Provide pseudo code for solving the single-source shortest path problem in an unweighted, connected undirected graph. What is the asymptotic performance of your algorithm? Justify your answer.
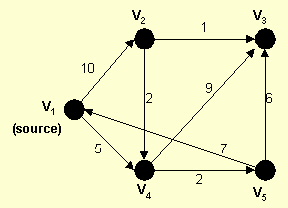
23. Run Dijkstra's algorithm on the following directed graph to complete the table below, where d(v) is the distance from the source node to the vertex v; p(v) is the immediate predecessor of vertex v in the path from the source node to v.
    Use vertex V₁ as the source node. What is the shortest distance and shortest path from V₁ to V₅?



Vertex	D(v)	P(v)
V1
V2
V3
V4
V5

24. Under what circumstances does Dijkstra's algorithm produce incorrect results for a weighted, directed graph? Give an example of such a graph.
25. Define HEAP.
26. State the Heap property. What implications does the heap property have for the values stored in the heap?
27. Where are the largest, 2^nd largest, 3^rd largest and smallest elements located in a HEAP?
28. Explain how to modify HeapSort to sort in descending order.
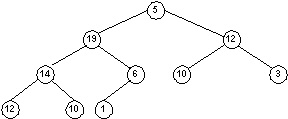
29. Which node in the following "heap" violates the heap property?

    Illustrate the calls to HEAPIFY () to restore the heap property.

    

30. Define hash table, collision, separate chaining, linear probing, primary clustering, hash function
31. Demonstrate the insertion of the keys 5, 28, 19, 15, 20, 33, 12, 17 and 10 into a hash table with collision resolved by chaining. Let the table have 9 slots and let the hash function be h(k) = k mod 9.
32. Illustrate the result of inserting the keys 10, 22, 31, 4, 15, 28, 17, 88 and 59 into a hash table of length 11 using open addressing with hash function h(k) = k mod 11 by completing the table below, where each column shows the contents of the hash table after inserting the value in the column heading.

Index	Empty	10	22	31	4	15	28	17	88	59
0
1
2
3
4
5
6
7
8
9
10