Homework

Homework accounts for 35% of the final grade. Homeworks are due every other Thursday (unless otherwise) and there will be 7 homeworks. All homeworks should be done individually unless otherwise mentioned. You are allowed to discuss and exchange ideas but should refrain from exchanging exact solutions. Rule of thumb is when you're sitting down to write/code, you should do it by yourself.

Late policy: Homeworks are either due the start of class or the end of day. The exact time will be specified per homework. Make sure you pay close attention to the deadline! For in class submissions, if you cannot make it to the class, you must make alternate arrangements to have someone submit it on your behalf. You get a grace period of 10 mins after which late penalty will apply. Late penalty is 40% as long as you turn it in by the start of the subsequent class. After this, your submission will not be graded.

Submission maybe paper or electronic and depends on the homework. Every homework will have the submission method mentioned at the start.

Submit system
For electronic submissions, we will use the umbc submit system. The submission method will be specified for each homework (sometimes individual questions!)
The class name is cs471_abhay1

THINGS TO REMEMBER

• All files will be .txt files unless otherwise mentioned.
• Filenames should simply be the question number from the homework with the .txt extension as shown below.
• The submit system allows submission until midnight of the due date but THE DEADLINE IS BEFORE CLASS ON THE DUE DATE. The scripts that will pull the homework files will check against the time stamp. Late penalties will apply if it is not submitted by the specified deadline in the hw description.

Use submitproj to look at the homeworks and the deadlines

linux2[32]% submitproj cs471_abhay1
The following projects are defined for abhay1's cs471_abhay1 class:
hw1		Homework 1. This should be submitted by 09/15/2016 1.10pm EST. 
	

You can then use submit to submit your files to the specific homework/project

linux2[114]% cd myhw1/
linux2[115]% ls
1.txt	2.txt	3.txt
linux2[116]% submit cs471_abhay1 hw1 1.txt 2.txt 3.txt
Submitting 1.txt...OK
Submitting 2.txt...OK
Submitting 3.txt...OK
	

Homework 1

Total points: 5 (5% of the final grade)
Due Date: 11:59pm EST, 15th September 2016
Submission method: Electronic
Submission hw name: hw1
Note - For question 2, feel free to watch the video in groups and discuss ideas. Especially if you have already formed your project group and are searching for ideas. However, when you're writing your essay, you must do it individually.

But first!

• Explore the course site.
• Accept the Piazza invite you received in your email.
• Make sure you have a unix account on the gl.umbc.edu machines and go through this tutorial to know how to use the umbc submit system.

1. (2.5 points)
   Lets chat with a bot!
   The Turing test is a behavioral approach to determining whether or not a system is intelligent. It was originally proposed by mathematician Alan Turing, one of the founding figures in computing. Turing argued in a 1950 paper that conversation was the key to judging intelligence. In the Turing test, a judge has conversations (via teletype) with two systems, one human, the other a machine. The conversations can be about anything, and proceed for a set period of time (e.g., an hour). If, at the end of this time, the judge cannot distinguish the machine from the human on the basis of the conversation, then Turing argued that we would have to say that the machine was intelligent.

   Things to do
   • Skim through the wiki article about the turing test - https://en.wikipedia.org/wiki/Turing_test
   • Chat with Clever bot - http://www.cleverbot.com/
   Things to turn in - ;
   1. Create a text file named 1.txt and paste your conversation with Clever bot.
   2. Create a text file named 2.txt and answer the following questions (50 words or less);
      1. Mention 2 things that surprised you!
      2. Mention 2 things that disappointed you!
      3. If you were the judge of the Turing test, would you think the bot would pass?

2. (2.5 points)
   What can AI do right now?
   Watch this fascinating TED talk from Jeremy Howard about the state of the art in AI & machine learning.
   
   Watch it on TED
   
   or Watch it here on YouTube

   
   Things to turn in - Create a text file named 3.txt and;
   Write a 250-350 word essay about how you think techniques from AI can be applied to your favorite domain?
   Couple of specific questions your essay should cover.
   • What are some of your favorite domains? (ex: football, music, literature, politics etc.)
   • What interesting goal do you wish to achieve from applying AI? (ex: predict football game results, predict election results, generate poetry/rap lyrics, self driving vehicles)

   p.s - The goal of this exercise is to help you think about ways to apply AI to domains you are really passionate about. This is also a good way for you to brainstorm potential ideas for your final project. Following submission, I will do some basic text analysis to get a sense of different topics the class is interested in and cluster students with similar ideas! (potential projectmates maybe?)

3. (0 points)
   Watch Big Hero 6! :)

Homework 2

Total points: 100 (5% of the final grade)
Due Date: 11:59:59pm EST, 29th September 2016
Late submission: 11:59:59pm EST, 4th October 2016 (40% penalty)
Submission method: Electronic
Submission hw name: hw2

Click to download the test cases and the OPTIONAL starter code!

1. (100 points)

   We will use Python to implement the following search algorithms: breadth first search, depth first search, uniform cost search, best first search and A* search.

   Some useful links to bootstrap yourself with python

   • Quick start
   • LearnPython.org - More comprehensive course
   • Interactive python
   • Codingbat.com - Practice problems

   Things to turn in - You will create a python file called search.py that should be run as shown

   python search.py algorithm_name node_file.txt edge_file.txt heuristics_file.txt start_node end_node output_file.txt

   • node_file.txt - This is the set of nodes where each line represents a single node.

     A
     B
     C
     D
     E
     F
     G
     

   • edge_file.txt - Each edge in the graph is represented in a single line as shown in the edge_file

     A B 5
     A C 20
     B E 2
     C F 3
     C G 10
     C D 10
     E C 3
     F E 1
     F G 2
     

     Note that A B 5 means that there is an edge from A to B that has a cost 5. It DOES NOT mean there is an edge from B to A.
   • heuristic_file.txt - This is the value of the heuristic function for each node to the goal node. This is only used for best first and A* search.

     A 2
     B 3
     C 1
     D 10000
     E 2
     F 1
     G 0
     

     The value indicates how close the heuristic function thinks the current node is from the goal node (i.e the cost from the goal node). Infinity is replaced by a large number.
   • algorithm - This argument specifies what algorithm has to be used and takes one of the following values.
     • breadth - Breadth First Search
     • depth - Depth First Search
     • uniform - Uniform Cost Search
     • greedy - Greedy Best First Search
     • astar - A* Search
   • startNodeName - The name of the start node e.g A
   • goalNodeName - The name of the goal node e.g G
   • output_file.txt - This is the output file you will have to write the results in. It must follow the following format. For example, BFS on the above graph from A to G will return

     A
     C
     G
     30
     

     The file must start with the start node on the first line followed by the subsequent nodes in the path in each line and terminate with the goal node. The last line should be the cost of the path.
     If there is NO path from the start to the goal node, your program must simply write "false" into the output file.

   NOTE - Nodes should be added to your stack or queue alphabetically, as we did in class. You should adhere to the specified output format since grading will be automated and incorrect format might mean you lose points!

   You are free to discuss approaches with your friends but you must code by yourself! Plagiarism detection software will be used so think twice before sharing/exchanging code

   You will submit using submit cs471_abhay1 hw2 search.py

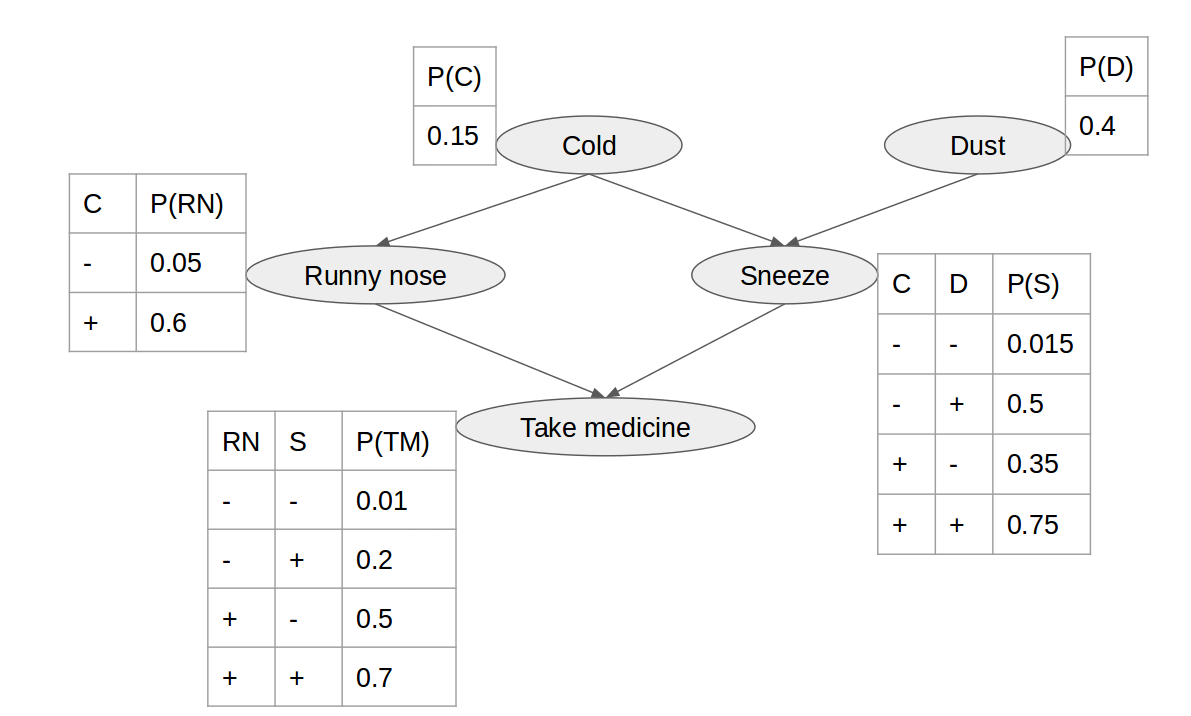
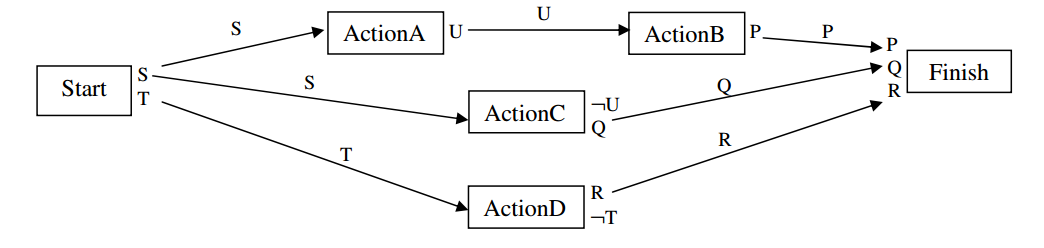
Homework 3

Total points: 100 (5% of the final grade)
Due Date: 1.10pm EST, 13th October 2016
Late submission: 1.10pm EST, 18th October 2016
Submission method: Paper (in class)/ Electronic (submit system - PDF FILES ONLY!)
Submission hw name: hw3

1. Answer each of the following questions in no more than a single sentence!

   (3 points each * 5 = 15)

   1. Given a function f(x) that defines the space, what is the update function for gradient descent? (the next value to go to)
   2. Give one way to deal with local optima for gradient descent.
   3. How many optima does the function f(x,y)= x^2 + y^2 have?
   4. What is the significance of "temperature"(T) in simulated annealing?
   5. What is the purpose of mutations in Genetic algorithms?

2. Consider the minimax tree shown below

   

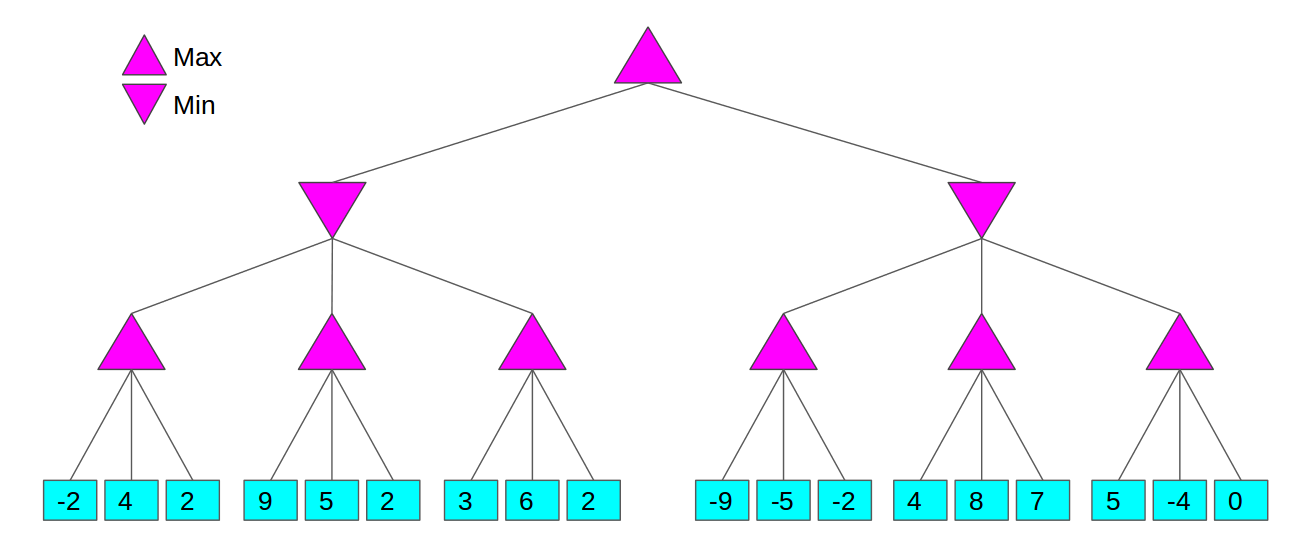
   1. (5 points) Use the minimax algorithm to fill in values for each of the nodes. Indicate the optimal path taken from the root node to the leaf node (using arrows)

   2. (20 points) Use the alpha-beta pruning with minimax algorithm on the same tree.

      • For each max node, write down the changes of the value of alpha
      • For each min node, write down the changes of the value of beta
      • Show pruned nodes with a single horizontal line across the node
      • How many nodes were successfully pruned? (including non-leaf nodes)

3. Consider the following CSP

   • 4 Variables: X1, X2, X3, X4
   • Domains:
     • D1 = {1, 2, 3, 5}
     • D2 = {2, 3, 4, 8}
     • D3 = {4, 5, 7, 8}
     • D4 = {0, 1, 2, 4, 7, 9}
   • Constraints:
     • X1 >= X2
     • X2 > X3 or (X3 - X2) = 3
     • X4 < X3

   Answer the following questions

   1. (5 points) Draw the constraint graph
   2. (5 points) Is the network arc consistent? Justify
   3. (20 points) Run the AC3 algorithm to make the network arc consistent. Things to show at each step of the algorithm:
      • Queue status
        Hint: Each ordered pair of constrained variables is added into the queue.
Eg: [(X1,X2), (X2,X1), (X1, X3), (X3, X1)]
      • The domain values
        Hint: After each pair of variables from the queue is processed, their corresponding domains are reduced to ensure arc consistency

4. Consider the following scenario: Your partner finds several inappropriate text messages on your phone and gets suspicious that you are cheating. You try to convince him/her that it is some random person but he/she asks you to prove it by taking a lie detector test!

   You get an at-home lie detector that has the following information on the box. It boasts a true positive accuracy of 97% i.e. the probability of you failing the lie detector test if you did indeed cheat is 0.97 . In tiny font, it also lists its false positive rate of 2.5% i.e. the probability of you failing the test even if you didn't actually cheat is 0.025 .

   He/she quotes a tabloid magazine that says "3 out of 10 people cheat on their partners" and vows to break up if the probability that you cheated after taking the test is more than 0.1 . The test is administered and behold, you fail!

   (10 points)

   1. What is the probability that you cheated before you even took the test? (prior)
   2. What is the probability that you cheated after you failed the test? (posterior)

   Failing the lie detector test makes you start to panic! You start to search online and find a credible research study that concludes "Only 1 in 1000 CS students actually cheat on their partners because they tend to have no life outside of coding". You get excited because you are a CS student!

   (10 points)

   1. Can you convince your partner to stay with you using probabilistic arguments? (what is the probability that you have cheated given this new information?)

   Your partner is still not convinced! He/she asks you to take the test again and behold, you fail again!

   (10 points)

   1. Assuming the two tests were independent of each other, could you still convince your partner to not break up with you? (what is the probability that you have cheated given you failed twice and you're a CS student?)

Homework 4

Total points: 100 (5% of the final grade)
Due Date: 11.40am EST, 3rd November 2016
Late submission: 11.40am EST, 7th November 2016
Submission method: Paper (in class)/ Electronic (submit system - PDF FILES ONLY!)
Submission hw name: hw4

1. Consider the Bayes network below where all the variables are binary. '-' represents negative or False & '+' represents positive or True. The tables are corresponding conditional probability distributions.

   
   1. (5 points) State if the following statements are True or False.
      1. C (cold) and D (Dust) are independent.
      2. S (sneeze) and RN (runny nose) are independent.
      3. S (sneeze) and RN (runny nose) are independent given C (cold) is - .
      4. TM (take medicine) and C (cold) are independent.
      5. TM (take medicine) and C (cold) are independent given S (sneeze) is +
   2. (10 points) Use enumeration to compute the probability that a person takes medicine (TM=+) given he/she has a runny nose (RN=+) and there isn't any dust (D=-). Show the steps of enumeration.
   3. (10 points) Sampling: Use a random number generator https://www.random.org/ to generate numbers between 1-100. Assign numbers to the variables based on the probabilities i.e. P(C) = 0.15 so numbers 1-15 will indicate C=+ while 16-100 indicate C=-. Generate 5 samples (by assigning + or - based on the number generated) for all the variables. From your 5 samples, what is the probability that a person takes medicine i.e TM=+? Also what is the probability that TM=+ given D=-.
2. (25 points) You are a herpetologist and you've discovered a new species of lizard! To understand its growth, you measure its length every month. Here is the data for the first three months

   age (month)	length (inches)
   1	4
   2	5.5
   3	7

   The lizard is now 4.5 months old. Before measuring the length, you decide to predict its length.
   You use linear regression and come up with a function to determine the length as length = 3 * age + 1.
   You also ask your statistician friend and he comes up with the function length = 2 * age + 2.
   
   1. (20) Which is a better function for the given data? (Compute the training error for each function)
   2. (5) Using the better of the two functions, what would you predict the lizard's length to be? (remember it is 4.5 months old now)
3. (25 points) Consider the following table with two features X1 and X2 for some output variable Y

   X1	X2	Y
   T	T	T
   T	F	F
   T	F	T
   F	T	F
   T	F	T
   F	F	T
   T	T	T

   If you were building a decision tree, which attribute would you prefer for your first split? X1 or X2? Justify your decision by computing the Information Gain for both the attributes.
4. (25 points) You are given the following data points in 2D space:
   d1=(1,1), d2=(2,4), d3=(3,2), d4=(6,4)
   You are running k-means clustering with k=2. Lets say the two cluster-centers were randomly initialized to
   cluster1 center = (0,8), cluster2 center = (9,7)
   After the first iteration of k-means,
   • (20) What are the new cluster centers?
   • (5) What cluster is each data point (d1,d2,d3,d4) assigned to?

Homework 5

Total points: 100 (5% of the final grade)
Total points possible: 140 (40 points extra credit)
Due Date: 11.59pm EST, 18th November 2016
Late submission: 11.59pm EST, 22nd November 2016
Submission method: Electronic only(PDF only)
Submission hw name: hw5

Homework 5 is on Google Drive.

Link: https://docs.google.com/document/d/1bDHVMGu-N5alKpiA79gsidM7bnpVSPG18X7GX2Tgs5A/edit?usp=sharing

Homework 6

Total points: 100 (5% of the final grade)
Total points possible: 120 (20 points extra credit)
Due Date: 11.40pm EST, 1st Dec 2016
Late submission: 11.40pm EST, 6th Dec 2015 (electronic only)
Submission method: Paper (in class)/ Electronic (submit system - PDF FILES ONLY!)
Submission hw name: hw6

1. For each of the following expressions in propositional logic, state if they are syntactically correct or not. (Yes/No)

   (2 points each * 5 = 10)

   1. Q ⇒ P ∧ Q ∧ R
   2. ((P ∧Q) ∧ R) ⇔ [P ∧ (Q ∧ R])
   3. (Birds Fly ¬ ⇒ Pengiuns Fly)
   4. (P ⇒ ¬Q) ∨ (¬Q ⇒ P)
   5. Santa is home ∧ ∨ Rudolf is hungry

2. Use the following atomic propositions and express the given English sentences into well formed propositions of propositional logic

   • Baltimore is a city = BaltimoreIsCity
   • Baltimore is large = BaltimoreIsLarge
   • Baltimore is in Maryland = BaltimoreIsInMaryland
   • Baltimore borders the Chesapeake bay = BaltimoreBordersChesapeakeBay

   (2 points each * 5 = 10)

   1. Baltimore is not a city if Baltimore is not large
   2. Baltimore is a large city in Maryland
   3. If Balitmore borders Chesapeake bay, then Baltimore is in Maryland
   4. Baltimore is large if and only if it is a city or it borders the Chesapeake bay
   5. Baltimore borders the Chesapeake bay, but is not in Maryland

3. For the following statements, state if it is valid, satisfiable or a contradiction

   (2 points each * 5 = 10)

   1. (Smoke ⇒ Smoke) ∧ (Smoke ∧ ¬ Smoke)
   2. (Smoke ∨ ¬ Smoke) ∨ (Smoke ⇒ Fire)
   3. (Smoke ⇒ Fire) ⇒ (¬Smoke ⇒ ¬Fire)
   4. (Smoke ⇒ Fire) ⇒ ((Smoke ∧ Heat) ⇒ Fire)
   5. Big ∨ Dumb ∨ (Big ⇒ Dumb)

4. Translate the following English sentences into First order Logic

   (3 points each * 10 = 30)

   1. There is a bunny who is cute
   2. Every cloud has a silver lining
   3. People who play GTA don't like people who play candy crush
   4. Every child who has a Chinpokomon card is cool
   5. No person can own a dog and hate animals at the same time
   6. For every action, there is an equal and opposite reaction
   7. Everyone needs somebody sometime
   8. Deep roots are not killed by the frost
   9. No number is less than zero
   10. There is no number such that no number is less than it

5. Convert the following FOL sentences to english

   (2 points each * 5 = 10)

   1. ∀x IsABunny(x) ⇒ IsCute(x)
   2. ∀x EatsRamen(x) ⇒ IsHomeless(x) ∨ IsAGradStudent(x)
   3. ∃s ∀h IsAStudent(s) ∧ IsTaking(s, AI) ∧ HomeworkFor(h, AI) ∧ ¬Hates(s,h)
   4. ∀z (IsACat(z) ⇒ Rules(z)) ∧ (IsADog(z) ⇒ Drools(z))
   5. ∃time ∀base isACaptain(JackSparrow) ∧ isABase(base) ∧ lesser(time,Now) ∧ Owns(JackSparrow, base, time) ⇒ Owns(Cats, base, Now)
6. (50 points)

   1. Represent the following knowledge base in first-order logic. Use the predicates attend(x), fair(t), pass(x, t), prepared(x), smart(x), study(x), umbc-student(x), where arguments x have the domain of all students and arguments t have the domain of all tests

      • Everone who is smart, studies and attends class will be prepared.
      • Everyone who is prepared will pass a test if it is fair
      • Every UMBC student is smart
      • If a test isn't fair, no one will pass the test
      • Coco is a UMBC student
      • At least one student passed the 471-exam
      • Coco attends class
   2. Convert this knowledge base into conjunctive normal form
   3. Prove that

      study(Coco) => pass(Coco, 471-exam)

      using resolution refutation. Show your proof as a series of sentences added to the KB. Clearly show which sentences were resolve to product each new sentence and what the unifier was for each resolution step. (Similar to the one on the slides)

Homework 7

Total points: 100 (5% of the final grade)
Total points possible: 120 (20 points extra credit)
Due Date: 1.10pm EST, 13th Dec 2016
Late submission: NO LATE SUBMISSION ALLOWED
Submission method: Paper (in class)/ Electronic (submit system - PDF FILES ONLY!)
Submission hw name: hw7

1. STRIPS Planning

   In the monkey-and-bananas problem, a monkey is in a laboratory with some bananas hanging out of reach from the ceiling. The monkey’s goal is to get the bananas. A box is available that will enable the monkey to reach the bananas if he climbs on it. Assume that your domain predicates are:

   • At(x,l): x is at location l
   • Height(x,h): x has height h
   • Holding(x,o): x is holding object o
   • Box(o): object o is a box
   • On(x,o): x is on object o

   Initially, the monkey is at location A, the bananas at B, and the box at C. The monkey and box have height Low, but if the monkey climbs onto the box, he will have height High, the same as the bananas. The actions available to the monkey include Go from one place to another, Push a box from one place to another, ClimbUp onto or ClimbDown from a box, and Grasp or Ungrasp an object.

   1. (10 points) - Using STRIPS syntax, write down the initial state description and the goal.
   2. (20 points) - Using STRIPS, write down definitions of the six actions. Ensure that all reasonable constraints are applied to the use of actions. For example, the monkey may only push or climb on a box if it is at the same location as the box, the monkey may only change locations if he is on the ground (i.e., has height Low), and grasping results in holding the object if the monkey and object are in the same place at the same height.

2. (20 points) Consider the inconsistent partially ordered plan below. Identify the conflicts in this plan and show all ways of resolving them that follow the principle of least commitment. For each solution, draw the new partially ordered plan, and list all of its linearizations

   

3. Partially solve 2015 Final exam

   Exam link: 2https://docs.google.com/document/d/1C5Q8YHd1es-A26yTQkVPb3oWJxOA8fn-1BamkR4QIio/edit?usp=sharing

   Answer the following questions from the last year's final (the solutions have been removed)

   1. (20 points) - Question 2 - Decision Trees
   2. (20 points) - Question 4 - Logistic Regression (the points on the exam was 15 but for HW7 its 20; 5 for each subquestion)
   3. (10 points) - Question 6 - KNN classification
   4. (20 points) - Question 7 - First Order Logic