The DLX processor has 32 registers, each of which is 32 bits long.
However, two of these registers are reserved for special purposes.
Register 0 always contains zero. It can be used as a source operand
whenever zero is needed, and stores to it have no effect. Register 31
is reserved for use by some DLX instructions, as will be described
shortly. DLX also has a 32 bit program counter.
| Instr. |
Description |
Format |
Opcode |
Operation (C-style coding) |
|---|
| ADD |
add |
R |
0x20 |
Rd = Rs1 + Rs2 |
| ADDI |
add immediate |
I |
0x08 |
Rd = Rs1 + extend(immediate) |
| AND |
and |
R |
0x24 |
Rd = Rs1 & Rs2 |
| ANDI |
and immediate |
I |
0x0c |
Rd = Rs1 & immediate |
| BEQZ |
branch if equal to zero |
I |
0x04 |
PC += (Rs1 == 0 ? extend(immediate) : 0) |
| BNEZ |
branch if not equal to zero |
I |
0x05 |
PC += (Rs1 != 0 ? extend(immediate) : 0) |
| J |
jump |
J |
0x02 |
PC += extend(value) |
| JAL |
jump and link |
J |
0x03 |
R31 = PC + 4 ; PC += extend(value) |
| JALR |
jump and link register |
I |
0x13 |
R31 = PC + 4 ; PC = Rs1 |
| JR |
jump register |
I |
0x12 |
PC = Rs1 |
| LHI |
load high bits |
I |
0x0f |
Rd = immediate << 16 |
| LW |
load woRd |
I |
0x23 |
Rd = MEM[Rs1 + extend(immediate)] |
| OR |
or |
R |
0x25 |
Rd = Rs1 | Rs2 |
| ORI |
or immediate |
I |
0x0d |
Rd = Rs1 | immediate |
| SEQ |
set if equal |
R |
0x28 |
Rd = (Rs1 == Rs2 ? 1 : 0) |
| SEQI |
set if equal to immediate |
I |
0x18 |
Rd = (Rs1 == extend(immediate) ? 1 : 0) |
| SLE |
set if less than or equal |
R |
0x2c |
Rd = (Rs1 <= Rs2 ? 1 : 0) |
| SLEI |
set if less than or equal to immediate |
I |
0x1c |
Rd = (Rs1 <= extend(immediate) ? 1 : 0) |
| SLL |
shift left logical |
R |
0x04 |
Rd = Rs1 << (Rs2 % 8) |
| SLLI |
shift left logical immediate |
I |
0x14 |
Rd = Rs1 << (immediate % 8) |
| SLT |
set if less than |
R |
0x2a |
Rd = (Rs1 < Rs2 ? 1 : 0) |
| SLTI |
set if less than immediate |
I |
0x1a |
Rd = (Rs1 < extend(immediate) ? 1 : 0) |
| SNE |
set if not equal |
R |
0x29 |
Rd = (Rs1 != Rs2 ? 1 : 0) |
| SNEI |
set if not equal to immediate |
I |
0x19 |
Rd = (Rs1 != extend(immediate) ? 1 : 0) |
| SRA |
shift right arithmetic |
R |
0x07 |
as SRL & see below |
| SRAI |
shift right arithmetic immediate |
I |
0x17 |
as SRLI & see below |
| SRL |
shift right logical |
R |
0x06 |
Rd = Rs1 >> (Rs2 % 8) |
| SRLI |
shift right logical immediate |
I |
0x16 |
Rd = Rs1 >> (immediate % 8) |
| SUB |
subtract |
R |
0x22 |
Rd = Rs1 - Rs2 |
| SUBI |
subtract immediate |
I |
0x0a |
Rd = Rs1 - extend(immediate) |
| SW |
store woRd |
I |
0x2b |
MEM[Rs1 + extend(immediate)] = Rd |
| XOR |
exclusive or |
R |
0x26 |
Rd = Rs1 ^ Rs2 |
| XORI |
exclusive or immediate |
I |
0x0e |
Rd = Rs1 ^ immediate |
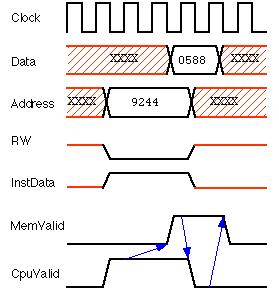
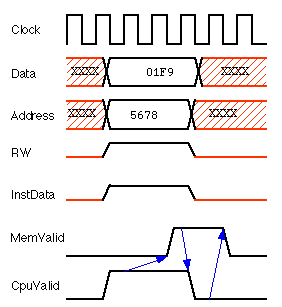
Once your CPU is working, however, you may want to use a "real" clock.
If so, you can create one in the simulator. However, make sure your
cycle time is sufficiently long. If it isn't, your CPU may not work.
![[Back]](http://www.cs.umbc.edu/~elm/gif/back-btn.gif) Go back to the main page.
Go back to the main page.