Project 3 - the 8-Puzzle
| Assigned | March 28, 2012 |
| Due | 11:59pm April 17, 2012 |
| Points | 100 |
| Updates | April 11, 2012 More sample output provided. |
Objectives
- To implement Priority Queue ADTs
- To apply priority queues to a difficult problem and measure the time and performance
- To implement a classic search algorithm to solve a problem
Background
Searching has been used as an effective method to solve complex problems whose solutions are within a huge space (i.e. there are lots of possibilities which may or may not be a solution). A search typically starts with the initial state S0 that satisfies the initial problem conditions and continuously generates new states from S0 and its descendents until the problem's goal state Sg that satisfies the solution conditions is generated. (In some problems there may be more than one goal state, but not in our project). A new state Sj is generated from a known state Si (initially only S0 is known) by an applicable "generation operator", and we say that Sj is a child of Si. A state is called an open state if none of its children have been generated, a closed state if all of its children have been generated, and a dead state if it is not a goal state and it cannot have a child (i.e., no generation operator is applicable to that state). The path (i.e. the set of states) from S0 to Sg is a solution to the problem. In this project we will be implementing a search method known as best-first to solve a child's puzzle.
Description
A simple but challenging child's hand-held toy is a small square plastic board known as the 8-puzzle. (A larger 15-puzzle is also available). In an 8-puzzle, there are 9 positions, one of which is empty with the others occupied by small, movable "tiles" numbered 1 — 8. The tiles may be moved horizontally or vertically to the empty position (thereby creating a new empty position). When the tiles are arranged in some predetermined ending position you win.
In this project, you are asked to implement a search method, called the best-first method to solve the 8-puzzle problem. This search method is supported by a priority queue. Given an initial configuration, S0, of 8 numbered tiles, 1, 2, —, 8, on a 3 x 3 board, move the tiles in such a way so as to produce a desired goal configuration, of the tiles, Sg, using the smallest number of moves (states).
Your project will be executed with a single command line argument which is the name of a data file that contains the initial state, S0, and the goal state Sg. See below for details of the command line and data file.
Best-first search
One of the search methods that guarantees to find the optimal solution (i.e., the one with the shortest solution path) is called best-first search. Best-first search requires that each state has an associated merit value measuring how likely it is to be on an optimal solution path. The general best-first search can be outlined as follows:
openQ = {S0} //the set of open states, initially contains only S0
while openQ is not empty
{
Sk = the state in openQ with the best merit value; // this is why it is called best-first
openQ = openQ — {Sk}; //remove Sk from openQ;
if Sk is a goal state, a solution has been found, so exit;
if Sk is a dead state, do nothing;
else generate all children of Sk, calculate their merit values, and insert them into openQ.
// Sk is now a closed state , since all of its children are open
// do not insert Sk's parent into openQ
}
Some details of this method such as how to generate the solution path once a goal state is reached and what is required for a good merit value function are not described here since they are not relevant to this project. But it is clear that if we treat the merit value of each state as its priority, then a priority queue is naturally a good choice for the openQ.
Generation operators
At each move, one of the numbered tiles adjacent to the empty position (either vertically or horizontally) can be moved to the empty position (and its previous position becomes empty). These moves are the legal generation operators since each move generates a new configuration (a child state).
An easier way to describe the operators is to consider the empty position as a blank tile and allow the blank tile to move up, down, left, or right one cell unless it hits the boundary. Depending on where the blank tile is located, a state can have 2, 3, or 4 children.
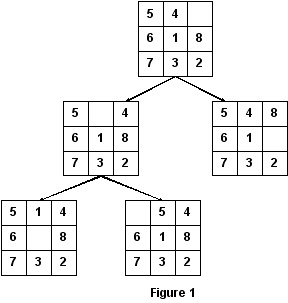
Figure 1 below is an example showing how child states are generated. Note that this initial state (at the top) has the blank tile on a corner, so it has two children. The child on the left has three children, one of which is the initial state. For efficiency, your implementation should NOT allow any state to generate its parent state as its child.
In this figure, there are two closed states (internal nodes) and three open states (leaf nodes) with path lengths from the initial state 2, 2, 1 (from left to right).
Merit Value Function
The merit value of each state is measured by a cost function (the smaller the better). For the 8-puzzle problem, The cost function for a state consists of two parts — how many moves have we made to get to the current state and how close do we think the current state is from the goal state.
cost(Si) = g(Si) + h(Si) where
g(Si) is the length of the path (number of moves/states) from S0 to state Si created during the search, measuring the cost from S0 to Si. Note that if Sj is generated from Si then g(Sj) = g(Si) + 1.
and
h(Si) is a heuristic that estimates the cost from Si to the goal state. In particular, h(Sg) = 0 and h(dead-state) = ∞.
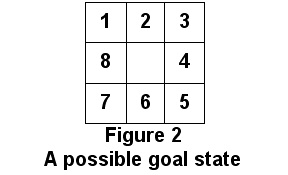
There are a number of good heuristics, h(Si), for the 8-puzzle problem. For this project, we use one of the simplest (and least efficient), which is to count the number of misplaced tiles in Si compared with their positions in the goal state Sg. For example, for the goal state in Figure 2 below, the h value for the open state at the lower-left of Figure 1 above is 7 (only one tile, #7, is in the goal position, so seven tiles are not in their goal position), and the total cost is therefore 2 + 7 = 9. Note that h does not count the blank tile because when all 8 numbered tiles are in their goal positions, the blank tile will also in its goal position.
When the goal state is reached at the end of a successful search, cost(Sg) = g(Sg) is the length of the solution path found from S0 to Sg. This value can be viewed as a measure of the time complexity of this problem since the number of moves (states) generated is in O(2^ g(Sg)). The size of openQ increases when search progresses. Since there is no dead-state for the 8-puzzle game as described here (why?), openQ will never shrink before the goal state is removed. The size of openQ at the end of the search thus can be viewed as the measure of the space complexity.
Your Tasks
You will have the following tasks:
- Check out your repository for Project 3.
- Edit the build.xml file as appropriate for this project.
- Implement a Priority Queue. You can base your
implementation on Priority Queue lecture slides and/or author's code of min
binary heap. The author's code may be found in Mr. Frey's public directory
/afs/umbc.edu/users/f/r/frey/pub/341/Project3/BinaryHeap.java
- Implement main( ) that validates the command line, reads the
data file and
performs the best-first search as descrived above to find the path from the initial
state to the goal state and produces the required output. Your best-fit implementation
MUST use a priority-queue as the openQ.
After the goal state is reached by the best-first search, your program will output
- The first five state configurations in the order they are removed from openQ, together with their cost, h value, and g value. If there are less than 5 states, print all of them.
- The solution cost (the length of the path you found from the initial state to the goal).
- The size of openQ at the end of the search process.
- Test your code with various data files. Feel free to post your data files and results on blackboard.
- Use the cvs utils to verify that your project has been submitted correctly.
Hints, Notes and other Requirements
- (H) Use the cost value as the priority for each state in openQ. Different states may have the same cost value, for uniformity, you should generate children of a state in the following order (if applicable): moving the blank tile up, left, down, right.
- (N) The same configuration can be generated from different paths, and thus with different cost values. You do NOT need to check if any has been generated before except that one state cannot have its parent as its child as stated earlier.
- (R) You must check command line arguments to ensure that they are valid, and that the command file can be opened. Eexit your program in case of error.
Command Line and Data File
Project 3 will be invoked with a command line with a single argument which is the name of the full path of the data file that contains a pair of state configurations.
The data file consists of 6 lines of 3 integers each. The first three lines form the initial state, the next three the goal state. Integers are 0 — 8 where 0 represents the blank tile, the other 8 are the numbered tiles. Integers on each line are separated by whitespace. Blank lines may appear anywhere in the file and should be ignored. The data file will not contain comments. You can assume the data file is free of syntax errors. The following is an example of a data file.
1 3 4 8 6 2 7 0 5 1 2 3 8 0 4 7 6 5
Sample Output
Buildfile: build.xml
run:
[java] [*]Initial state(S0)
[java] [*]======================
[java]
[java] 1 3 4
[java] 8 6 2
[java] 7 0 5
[java] Cost = 4
[java] g = 0
[java] h = 4
[java] [*]======================
[java] [*]Goal state (Sg) reached:
[java]
[java] 1 2 3
[java] 8 0 4
[java] 7 6 5
[java] Cost = 5
[java] g = 5
[java] h = 0
[java] [*]---------
[java] [*]Solution cost is: 5
[java]
[java] [*]Size of the openQ at end of search process: 7
[java]
[java] [*]First five states removed from openQ:
[java]
[java] [*]State #1
[java]
[java] 1 3 4
[java] 8 6 2
[java] 7 0 5
[java] Cost = 4
[java] g = 0
[java] h = 4
[java]
[java] [*]State #2
[java]
[java] 1 3 4
[java] 8 0 2
[java] 7 6 5
[java] Cost = 4
[java] g = 1
[java] h = 3
[java]
[java] [*]State #3
[java]
[java] 1 0 4
[java] 8 3 2
[java] 7 6 5
[java] Cost = 5
[java] g = 2
[java] h = 3
[java]
[java] [*]State #4
[java]
[java] 1 3 4
[java] 8 2 0
[java] 7 6 5
[java] Cost = 5
[java] g = 2
[java] h = 3
[java]
[java] [*]State #5
[java]
[java] 1 3 0
[java] 8 2 4
[java] 7 6 5
[java] Cost = 5
[java] g = 3
[java] h = 2
[java]
BUILD SUCCESSFUL
Total time: 1 second
Files to Be Submitted
Submit the following files. Please DO NOT submit your /bin directory or any .class files.
- build.xml
- Your source code (.java files) which must be organized in the way that is consistent with your build file, otherwise it won't compile and run
- An optional README file for notes to the TA
Grading and Academic Integrity
Project grading is described in the Project Policy handout. Note that proper class and method documentation via javadoc is required.
Cheating in any form will not be tolerated. Please re-read the Project Policy handout for further details on honesty in doing projects for this course.
This project is worth 100 points.
- 75 points - functionality (see below)
- 15 points - OO design and coding style
- 10 points - javadoc
- Basic Tests which may include, but are not limited to
- A puzzle with a simple solution that requires only a few moves
- Complex Tests which may include, but are not limited to
- A puzzle with a solution that is not obvious and requires several moves/states
- A puzzle in which one or more states can be generated via multiple paths.
- Atypical Tests which may include, but are not limited to
- a puzzle for which the initial state and the goal state are the same.
- a data file that cannot be opened
- Stress Tests which may include, but are not limited to
- a puzzle that requires a large number of moves/states