CMSC 341 Spring 2009
Project 3

"file1.txt 5 5 file2.txt"

Objectives

1. To gain experience implementing a Binary Tree ADT from scratch
2. To gain experience using inheritance with generic classes
3. To gain experience using Tree Iterators
4. To gain experience using a Binary Tree in a real application
5. To gain experience implementing the Adapter Design Pattern

Description

A Binary Search Tree is most commonly used for maintaining information in a manner such that any node's left child is less than that of its value and a right child is greater than it. This definition is recursive and visually creates a partitioning of data held within the structure. A Binary Space Partition Tree is an implementation upon this which is commonly used in graphics to divide a scene up about a specific polygon into all polygons that are either behind or infront of that specific polygon. For a polygon, or anything (an object), to be in view (visible to us) we commonly say you are facing it. For an object to be infront of you, we commonly refer to objects that are in view from our left shoulder to the right. In this project you will implement a variation upon both of these data structures creating a Space Tree which will be used to partition objects in a scene based upon a viewing location and view direction vector.

We will implement a variation of a binary search tree using inheritance called a Space Tree. This will require you to implement your own Binary Search Tree ADT and create the derived Space Tree implementation. This Space Tree has a couple of properties (some recursive) that must be upheld at all times given the following information:

The viewer is located at an object in Cartesian space. The point at which the viewer resides is indicated (x,y) The view vector consists of (dx,dy) which represents the run and rise of the direction in which the viewer is facing/directed.

Space Tree Properties:

• The Root is always the point at which the viewer resides, initially (after creation) this will be at an object in Cartesian space
• A node's right child is an object infront of the node applying the viewer's vector
• A node's left child is an object behind of the node applying the viewer's vector

Figure 1: All letters are objects in the scene. X is the object where viewer resides at that specific time. v is the view vector of the viewer. If we look at the children of Y, we can see the effect of applying v to Y. Note that E is infront of Y thus its right child, and D is behind Y making it its left child.

Distance and View Vectors

Calculates the distance between any two points

Given the view vector of the Space Tree v knowing if an object is in view (infront or behind) is a simple comparison.

Figure 2

First, we apply the viewer's view vector v to a node(object) and call this vector v' at P₀. Then given any point P₁, not currently present in our tree, we calculate another vector v₁

v1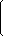

=

P1(x) - P0(x) P1(y) - P0(y)

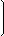If v₁ is not within a 90^o rotation of v' then it is out of view and behind P₀. Seen in Figure 2. To find the Θ for the difference in rotation (90^o from v') lets look at how to rotate a vector v by &Theta degrees to create v^'':

v''

=

vx*cos(&Theta) - vy*sin(&Theta) vy *cos(&Theta) + vx*sin(&Theta)

Using v' and v₁ you can solve for &Theta . where v₁ and v^' are normalized.

&Theta = cos-1(v1 dot v')

v1 dot v' = v1(x)*v'(x)+v1(y)*v'(y)

Project 3 will be invoked with multiple command line arguments.

1. The first argument is the name of the text file which will contain the objects in the scene. These are to be inserted into the Space Tree in the order read from the file based on the 2nd and 3rd command line arguments. The first object in this file is to be inital viewer location.
2. The second argument is the view vector. Note this view vector may divide your scene any way you can draw a straight line. (Two integers)
3. The third argument is the name of a text file containing a series of commands.

The Commands

• PRINTSCENE - Prints the name of all objects in the scene starting with the object that is farthest out of view to farthest in view
• PRINTVIEW - Prints the name of all objects in view of the viewer starting with the object closet to farthest
• ADDOBJECT - Adds an object with Name and X Y coordinates
• MOVE - Moves the viewer along the vector to the next Ith object given integer value.
• ROTATE - Rotates the view vector given an integer value for the degree. A positive value will represent a counter clockwise rotation and negative will represent a clockwise rotation.
• REMOVEOBJECT - Removes the object at the viewer's current location moving the viewer to the next closest object in view

The ADTs

The Scene Object ADT

The Space Tree ADT

• printViewableObjects() - this functions prints all objects infront of the viewer.
• moveViewpoint(int) - this function moves the viewer location forward or backward along the veiw vector to the next closest scene object. Forward and backwards are denoted by positive and negative values. See project notes for a definition of closest.
• rotateView(int) - this will trigger your tree to recreate itself at the viewer's location with the new view vector calculated from the old vector
• insert(Scene Object) - this will insert of a scene object into the tree.

Basic Project Requirements

1. ALL TREES used in this project must be created from scratch. This includes tree iterators if you choose to use one. This means NO JAVA TREES or ITERATORS are permitted.
2. You create/modify your own tree, tree node, and tree iterator.
3. The Space Tree must be implemented using inheritance from the Binary Tree you create.
4. All possible exceptions discussed pertaining to Trees must be caught and dealt with appropriately. Your program should continue processing after an exception if at all possible.
5. Only the Space Tree class is instantiated in main( ) or in functions called from main( ).
6. You may include any private data and private functions to any class.
7. Be prepared for your code to work on large data sets.
8. The move function must result in a splay operation. You can use either top-down or bottom-up splay methods.
9. You must bulletproof your code as much as possible, e.g. making sure that the command line parameters are all valid, that the files named in it all exist, and that there is at least one report command. In case of invalid report parameters, your program should print them and a message indicating that the command is in error.

Project Notes and Hints

1. You may not use the java tree classes and will recieve 0 points in this event. However, you may use the material presented in class as a guide. This does not mean you can copy any code from the slides.
2. For this project you are to consider closest as an object in the Space Tree which is nearest to the partition line created by a node view vector.
3. One or more objects may neither be infront nor behind a node. In this event, we will always treat these nodes as behind based on their distance.
4. Only implement methodolgy you NEED in your base classes.
5. Trees are generic in type.
6. The move operation should not trigger a recreation (or a new tree construction) of your entire tree about the new viewer position.
7. To answer the questions with this project, you may need to implement code that is not required by the output of the project.
8. There are many ways to implement your tree ADT. Choose the most appropriate given the requirements of the Space Tree.
9. Adhere to and live by the K.I.S.S. principle.
10. This is not an easy project. Start early!!!
11. Good Luck!

Files To Be Submitted

Grading and Academic Integrity

Project grading is described in the Project Policy handout.
Cheating in any form will not be tolerated. Please re-read the Project Policy handout for further details on honesty in doing projects for this course.

Remember, the due date is firm. Submittals made after midnight of the due date will not be accepted. Do not submit any files after that time.