Project 3, 4th Case
When you perform a deleteMin() operation in a min-max heap, you remove the root and replace it with the last item. This part is just like an ordinary binary heap. The next step is to "trickle down" the min-heap levels (the even levels). Again this part is also very similar to the trickling down procedure in a binary heap, with the exception that you have to consider the values stored in four grandchildren rather than two children.
One difference in a min max heap is that you have to be careful about when you stop tricking down. Considering the example in Figure 1 below. We remove 18 at the root and replace it with 92. The four grandchildren to consider are 39, 27, 29 and 38. Since 27, the smallest of the grandchildren, is smaller than 92, we swap the two and arrive at Figure 2.
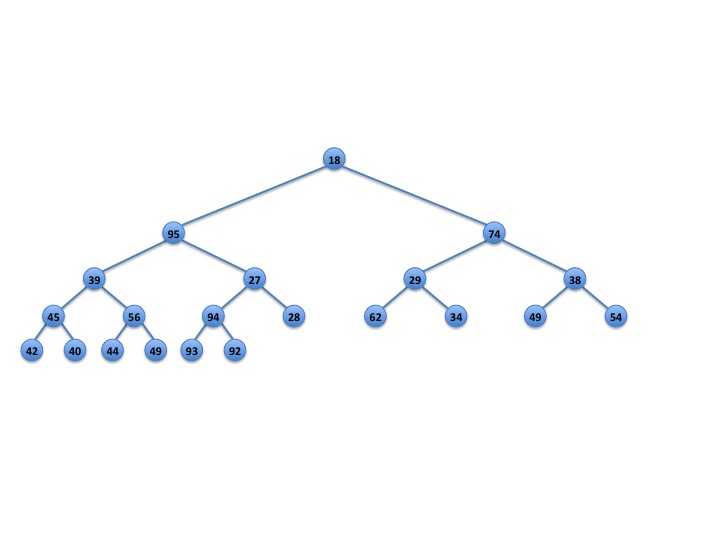
Fig. 1: original min-max heap before deleteMin()
Now consider Figure 2 below. The 92 cannot stay where it is, but you cannot determine this by looking at its grandchildren. This is a special case where the right child is a leaf and the left child is not. The minimum item in the right subtree is actually 28 — a child of 92, rather than a grandchild.
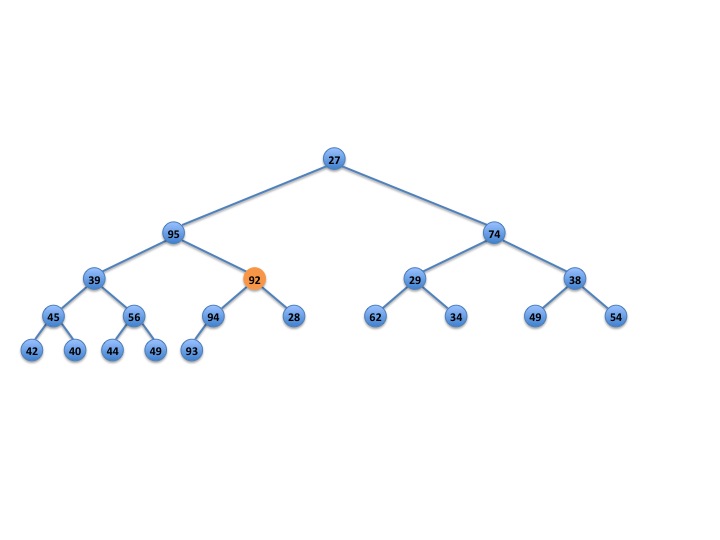
Fig. 2: Trickling down, but not quite done.
After swapping 92 and 28, we are finally done (Figure 3). Note that there is no possibility that 92 has to bounce further up the tree. That 95 is bigger than 92 is not a coincidence — 95 was originally the great-grandfather of 92 at an odd level. Also, we would not even have to consider this special case, if 92 did not trickle down to the same subtree from which it was removed.
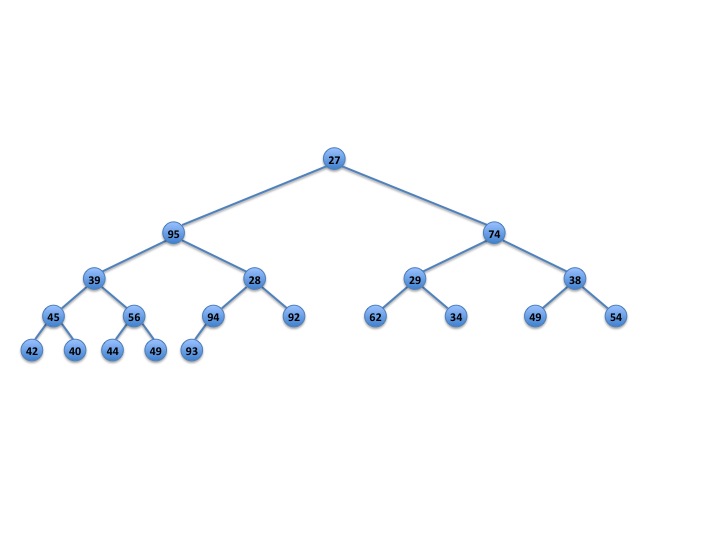
Fig. 3: Now we're done.
Another scenario might occur when we stop trickling down in case 4. In Figures 4–8, we perform a deleteMin() operation. We remove 18 and replace it with 48. Once again we stop trickling down before hitting bottom because the node in question has fewer than 3 grandchildren (Figure 5).
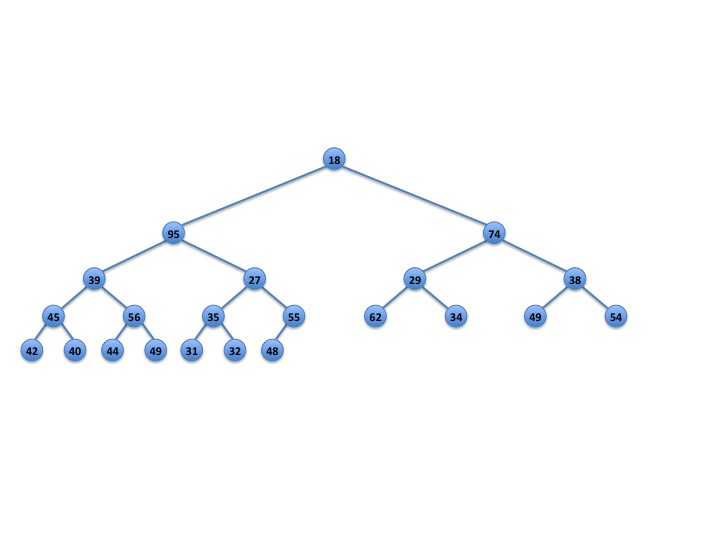
Fig. 4: Original min-max heap.
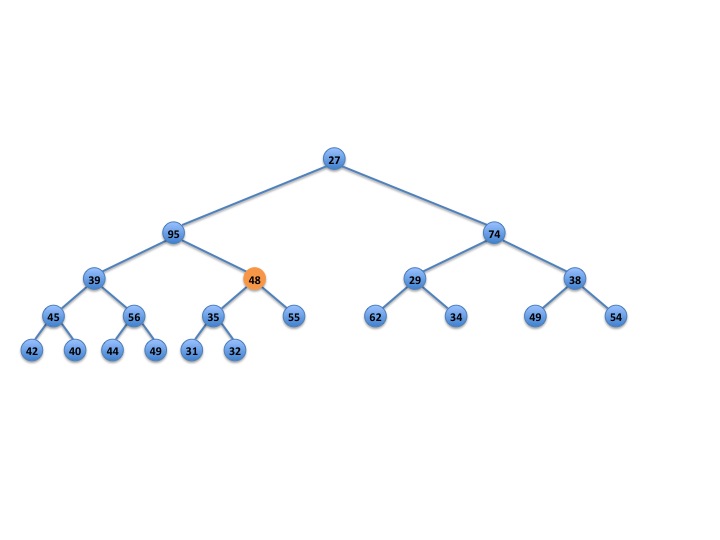
Fig. 5: After deleteMin() and trickling down stops.
This time 48 is swapped with a grandchild, 31. (Figure 6.) To complete the deleteMin() we still have to check whether 48 is smaller than its parent 35. It isn't so we swap 48 and 35. (This is what we would usually do in a deleteMin() operation and trickling down hits the last level.) After that we are done, since 48 is less than its grandparent 95.
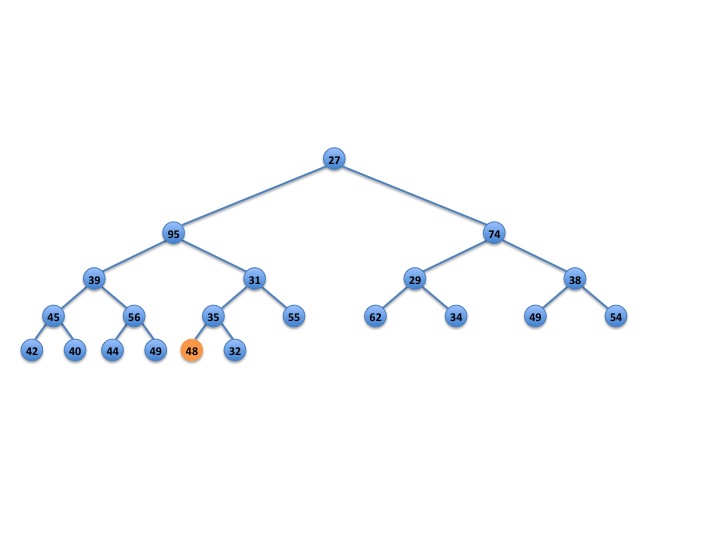
Fig. 6: This time we swap with the smallest grandchild, but we're still not done because 48 is bigger than 35.
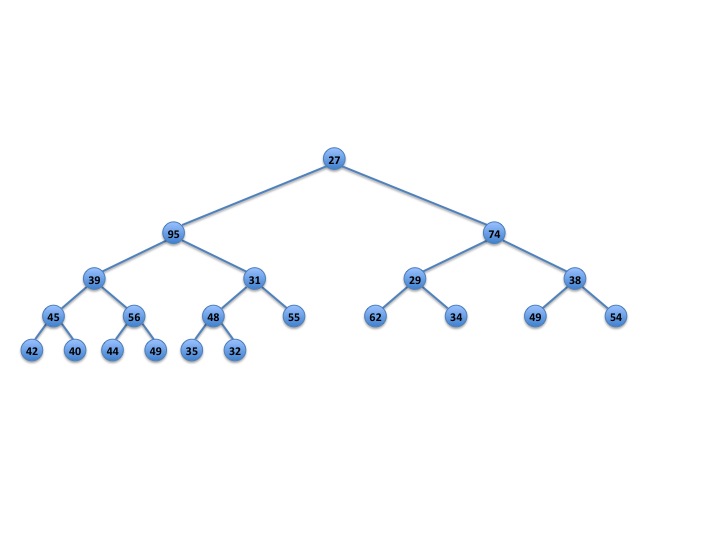
Fig. 7: We swap 48 with 35 and then we're done.