Homework 4

Due Dates:

Referenced exercises are from Data Structures and Algorithm Analysis in Java by Mark A. Weiss.

  1. Exercise 6.2: [Weiss, 3/e]

    1. Show the result of inserting 10, 12, 1, 14, 6, 5, 8, 15, 3, 9, 7, 4, 11, 13, and 2, one at a time into an initially empty binary heap.
    2. Show the result of using the linear-time algorithm to build a binary heap using the same input.

  2. Exercise 6.8: [Weiss, 3/e]

    Show the following regarding the maximum item in a min-heap with N items. (Note: A min-heap is a heap with smaller values stored closer to the root.)

    1. It must be at one of the leaves.
    2. There are exactly ⌈ N/2 ⌉ leaves. (Here ⌈ N/2 ⌉ is the ceiling of N/2.)
    3. Every leaf must be examined to find it.

  3. Exercise 6.18: [Weiss, 3/e]

    A min-max heap is a data structure that supports both deleteMin and deleteMax in O( log N ) time per operation. The structure is identical to a binary heap, but the heap-order property is that for any node X:

    at even depth:
    the element stored at X is smaller than or equal to the parent but larger than or equal to the grandparent
    at odd depth:
    the element stored at X is larger than or equal to the parent but smaller than or equal to the grandparent

    See Figure 1 below.

    1. How do we find the minimum and maximum elements?

    2. Show what happens to the min-max heap in Figure 1 after inserting 29, 4, 90, 5, 41, 9, 93 and 67. Show your work, then draw a clean copy of the final min-max heap.

      Hint: in a min-max heap, each element is in the interval between its parent and its grandparent. For example, 20 is between 17 and 80; 13 is between 12 and 52; 42 is between 28 and 87. At even and odd levels, the parent and grandparent swap places as the left or right endpoint of the interval.

      Another way to think about min-max heaps is that the even levels form a min-heap where a node's key is smaller than those stored in its grandchildren (up to 4 of them); and the odd levels form a max-heap where a node's key is larger than those stored in its grandchildren. (Note: not all min-heaps and max-heaps interlaced this way make a min-max heap, since interlacing does not guarantee the interval condition.)

      When you insert an item into a min-max heap, you add the new item at the last level, just like in a regular binary heap. However, you have to decide whether the item should percolate up the min-heap through the even levels or percolate up the max-heap through the odd levels. This is determined by comparing the new item with its parent.

    3. Show what happens to the min-max heap in Figure 1 after two deletemin operations. Also, show what happens to the min-max heap in Figure 2 after one deletemin operation. Finally, show what happens to the min-max heap in Figure 3 after one deletemin operation. Double check your answer and make sure that the interval condition is maintained at every node.

      Hint: deletemin for min-max heaps start out very much like deletemin in binary heaps. The root is replaced by the last item in the heap. This new item must then trickle down through the even levels of the min heap until it reaches "bottom". At the bottom, however, the interval condition might be violated because the new item is too big. This item may have to percolate up the max heap through the odd levels. When the new item reaches "bottom", you may have to check its parent or its children to see if the interval condition holds (depending on whether the last level is even or odd).

    4. Show what happens to the min-max heap in Figure 1 after two deletemax operations. Also, show what happens to the min-max heap in Figure 4 after one deletemax operation. Double check your answer and make sure that the interval condition is maintained at every node.

      Hint: deletemax for min-max heaps is analogous to deletemin.

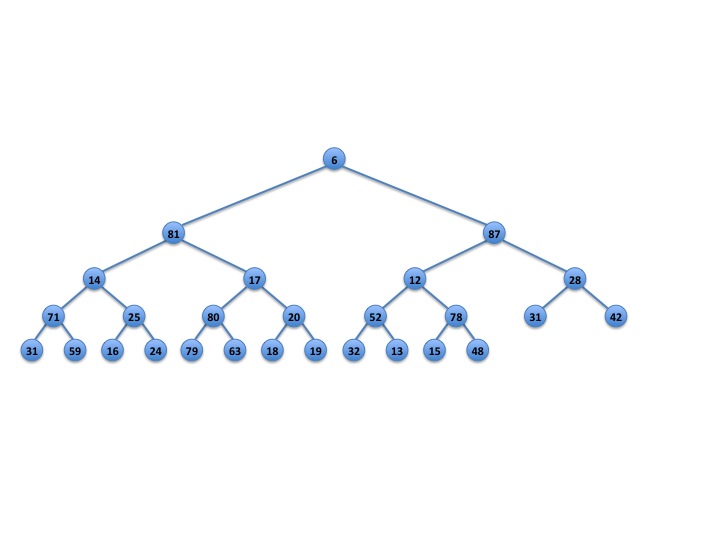
Fig. 1 [Fig. 6.57 from textbook]

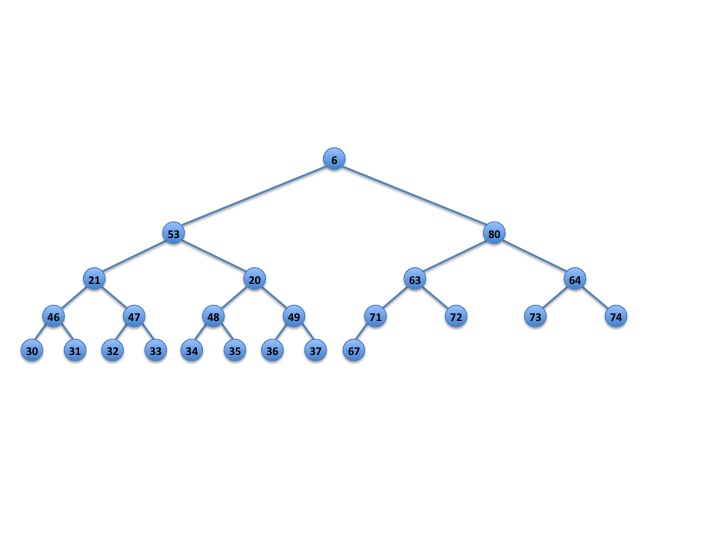
Fig. 2

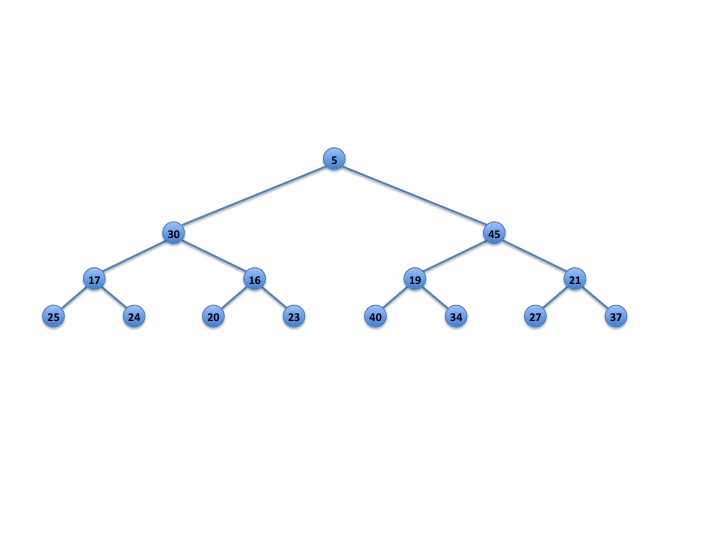
Fig. 3

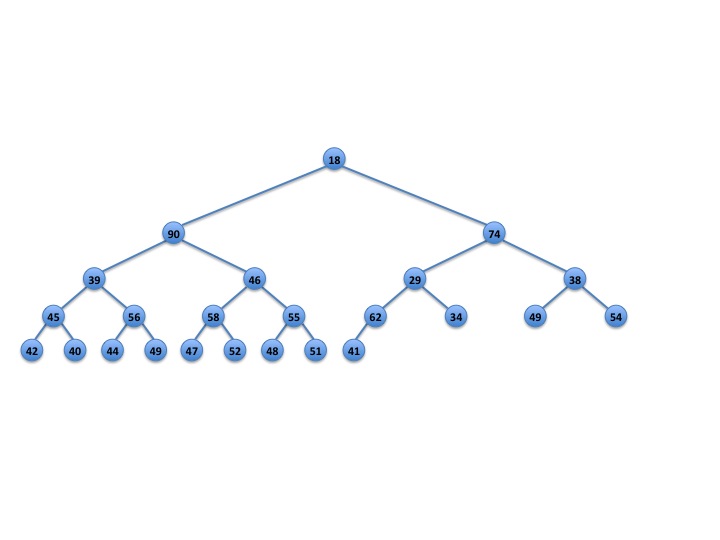
Fig. 4