Project 2 Spring '99

UMBC CS 201, Spring 99

UMBC CMSC 201 Spring '99

CMSC 201
Programming Project Two

Number Theory

Out: Wednesday 2/24/99
Original Due Date: Midnight, Wednesday 3/10/99

Snow Day Extension: Due: Midnight, Thursday 3/11/99

The Objective

The objective of this assignment is to get you familiar with writing and using functions in C and to heighten your appreciation of mathematics

The Background

The study of mathematics is separated into many fields. The one that leads the student to discover the beauty (yes, beauty) of mathematics is the field of number theory. This field deals with numbers and their relationships to each other and even to nature.

The field of number theory has lead to discoveries such as :

Prime numbers -- those which can only be divided by themselves and one. Primes of the form 2^p - 1, where p is prime are called Mersenne Primes after the French monk Marin Mersenne who discovered them. The search for Mersenne primes continues. You can participate in the search for new prime numbers by joining GIMPS (the Great Internet Mersenne Prime Search). The 37th and largest known Mersenne prime is 2^3021377 - 1.

Perfect numbers -- ancient mathematicians were interested in the relationship of a number and the sum of its divisors. A positive integer that is equal to the sum of its divisors (excluding itself) is called a "perfect" number. For example, the divisors of 6 are 1, 2 and 3. Since 6 = 1 + 2 + 3, 6 is a perfect number. The next three perfect numbers are 28, 496 and 8128. If the sum of the divisors is greater than the number, the number is called "abundant". If the sum of the divisors is less than the number, the number is called "deficient". Perfect numbers demonstrate some interesting properties -- all known perfect numbers end in 6 or 8; there are no known odd perfect numbers. Mersenne primes and perfect numbers are closely related.

Fibonacci numbers - the sequence 1, 1, 2, 3, 5, 8, 13, .... related to spirals, the birth of bunnies, branching trees and other
Fibonacci phenomena in nature

Triangular numbers -- many positive integers are considered geometric in nature. You learned about perfect squares in high school -- 1, 4, 9, 16. They are called "squares" because a group of 1, 4, 9 or 16 dots can be arranged in a square. Well, groups of 1, 3, or 6 dots can be arranged in a triangle and so these numbers are called "triangular" numbers. (If you've ever gone bowling, you'll recognize that 10 is also triangular.)
A more natural example arises when we consider a group of people who meet for the first time and everyone shakes hands with everyone else. The number of handshakes will be a triangular number.
Turns out that triangular numbers are the sum of consecutive integers.
To us this may just be an interesting relationship. To early Pythagoreans, it showed the mysterious nature of the universe and the way in which numbers and shapes have esoteric relationships.

The Golden Mean -- Also related to Fibonacci numbers, the Golden Mean (or Golden ratio or Golden section) is a ratio
( (1 + sqrt(5)) / 2) that represents the growth pattern of many things.

Positive integers can be categorized in many different ways.This project will let you investigate some familiar and some new ways of looking at integers.

The Task

Your mission is to write a program that examines the positive integers between 1 and 30 and categorizes them as follows.

ODD or EVEN
PRIME or COMPOSITE -- a prime number is an integer greater than one that is divisible only by itself and one. Any number that is not "prime" is "composite".
PERFECT/ABUNDANT/DEFICIENT --- as described above
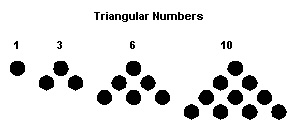
TRIANGULAR -- as described above

Your program will also count the number of integers from 1 to 30 that fall into each category and print a summary at the end.

Your program MUST include the following functions. Do NOT change the functions prototypes given below. You may choose to use more functions if you feel compelled to do so. It is not necessary to use any functions from the C math library. All "predicate" functions below should return 1 for TRUE and 0 for FALSE. You have some flexibility in implementing the other functions. Choose wisely (and use #defines)

int IsOdd (int n); -- a predicate function that returns TRUE if n is Odd and returns FALSE if it is not.
int IsPrime (int n); -- a prediate funtion that returns TRUE if n is prime, and FALSE if it is not
int IsDivisor (int a, int b); -- a predicate function that returns TRUE if a is a divisor of b, and FALSE if not
int SumDivisors (int n); -- returns the sum of the divisors of n.
int IsPerfect (int n); -- classifies n as "perfect", "abundant" or "deficient". A different value is returned for each different category.
int IsTriangular (int n); -- returns TRUE if n is a triangular number, FALSE if not
void PrintGreeting (void); -- displays a suitable greeting to the user

Sample Run

retriever[102] a.out This program classifies positive integers between 1 and 30 as Odd/Even, Prime/Composite, Perfect/Abundant/Deficient and Triangular Int Classifications..................................... 1 Odd Deficient Composite Triangular 2 Even Deficient Prime 3 Odd Deficient Prime Triangular 4 Even Deficient Composite 5 Odd Deficient Prime 6 Even Perfect Composite Triangular 7 Odd Deficient Prime 8 Even Deficient Composite 9 Odd Deficient Composite 10 Even Deficient Composite Triangular 11 Odd Deficient Prime 12 Even Abundant Composite 13 Odd Deficient Prime 14 Even Deficient Composite 15 Odd Deficient Composite Triangular 16 Even Deficient Composite 17 Odd Deficient Prime 18 Even Abundant Composite 19 Odd Deficient Prime 20 Even Abundant Composite 21 Odd Deficient Composite Triangular 22 Even Deficient Composite 23 Odd Deficient Prime 24 Even Abundant Composite 25 Odd Deficient Composite 26 Even Deficient Composite 27 Odd Deficient Composite 28 Even Perfect Composite Triangular 29 Odd Deficient Prime 30 Even Abundant Composite Between 1 and 30 there were 15 Odd integers and 15 Even integers 10 Prime numbers and 20 composite numbers 2 Perfect, 5 Abundant and 23 Deficient numbers 7 Triangular numbers retriever[103]

Although your output need not be identical to the above, all information (including the greeting) must be present.

Submitting the Program

You may name your source file for this project as you see fit.
To submit your project, type the following at the Unix prompt:

submit cs201 proj2 xxxxx.c (if you named your file xxxxx.c)

To verify that your project was submitted, you can execute the following command at the Unix prompt. It will show all files that you submitted in a format similar to the Unix 'ls' command.

submitls cs201 proj2

Sunday, 14-Mar-1999 18:25:27 EST