











Top-Down Design
Don Miner & Sue Evans
Adapted from the CS1 Course at Swarthmore College by Lisa Meeden
Press space bar for next slide












Don Miner & Sue Evans
|----[ | ]-----| min: 0 Q1: 4 median: 8 Q3:14 max: 19
# Filename: boxplot.py
# Author: Don Miner & Sue Evans
# Date: 8/22/09
# Section: All
# Email: bogar@cs.umbc.edu
#
# This program will produce a box plot for the
# numerical data the user provides either from
# a file or from typing at the terminal.
# printGreeting() prints an explanation of the program
# Inputs: none
# Output: none
def printGreeting():
print "\nThis program will produce a box plot"
print "for the numerical data you enter."
print "Welcome to my box plot program!\n"
# getInputFromUser() prompts the user for how he will
# give input, either from a file or from the terminal
# gets the input and returns it.
# Inputs: none
# Output: a list of numbers
def getInputFromUser():
print "In getInputFromUser()"
return []
# calculateStatistics() takes a list of numbers and
# calculates the minimum, the first quartile, the
# median, the third quartile and the maximum
# Inputs: a list of numbers called numbers
# Outputs: minimum, q1, median, q2, maximum
def calculateStatistics(numbers):
print "In calculateStatistics(numbers)"
return 1, 2, 3, 4, 5
# printBoxPlot() takes the 5 statistical values,
# prints them and the box plot for them.
# Inputs: minimum, q1, median, q2, maximum
# Output: none
def printBoxPlot(minimum, q1, median, q3, maximum):
print "In printBoxPlot(minimum, q1, median, q3, maximum)"
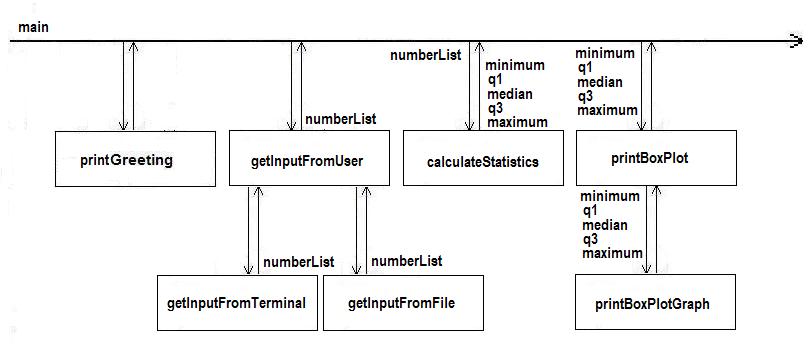
def main():
printGreeting()
numberList = getInputFromUser()
minimum, q1, median, q3, maximum = calculateStatistics(numberList)
printBoxPlot(minimum, q1, median, q3, maximum)
main()
linuxserver1.cs.umbc.edu[108] python box.py This program will produce a box plot for the numerical data you enter. Welcome to my box plot program! In getInputFromUser() In calculateStatistics(numbers) In printBoxPlot(minimum, q1, median, q3, maximum) linuxserver1.cs.umbc.edu[109]
|----[ | ]--| min: 0 Q1: 4 median: 8 Q3:9 max: 11
# printBoxPlot() takes the 5 statistical values,
# prints them and the box plot for them.
# Inputs: minimum, q1, median, q3, maximum
# Output: none
def printBoxPlot(minimum, q1, median, q3, maximum):
printBoxPlotGraph(minimum, q1, median, q3, maximum)
print "min:", minimum
print "Q1:", q1
print "median:", median
print "Q3:", q3
print "max:", maximum
# printBoxPlotGraph() takes the 5 statistical values
# and prints just the box plot graph for them.
# Inputs: minimum, q1, median, q3, maximum
# Output: none
def printBoxPlotGraph(minimum, q1, median, q3, maximum):
print " In printBoxPlotGraph(minimum, q1, median, q3, maximum)"
>>> "hello"*3 'hellohellohello' >>> "!"*5 '!!!!!'
# printBoxPlotGraph() takes the 5 statistical values
# and prints just the box plot graph for them.
# Inputs: minimum, q1, median, q3, maximum
# Output: none
def printBoxPlotGraph(minimum, q1, median, q3, maximum):
# find the sizes of the pieces
whiskerLeftSize = q1 - minimum
boxLeftSize = median - q1
boxRightSize = q3 - median
whiskerRightSize = maximum - q3
# construct the pieces
# the space before the minimum
blankLeft = ' ' * minimum
whiskerLeft = '-' * whiskerLeftSize
boxLeft = ' ' * boxLeftSize
boxRight = ' ' * boxRightSize
whiskerRight = '-' * whiskerRightSize
# concatenate the pieces
# break this into left & right so lines don't wrap
left = blankLeft + '|' + whiskerLeft + '[' + boxLeft + '|'
right = boxRight + ']' + whiskerRight + '|'
boxplot = left + right
print boxplot
printBoxPlotGraph(1, 3, 5, 8, 11)
|--[ | ]---|
# printGreeting() prints an explanation of the program
# Inputs: none
# Output: none
def printGreeting():
print "\nThis program will produce a box plot"
print "for the numerical data you enter."
print "Welcome to my box plot program!\n"
# getInputFromUser() prompts the user for how he will
# give input, either from a file or from the terminal
# gets the input and returns it.
# Inputs: none
# Output: a list of numbers
def getInputFromUser():
print "In getInputFromUser()"
return []
# calculateStatistics() takes a list of numbers and
# calculates the minimum, the first quartile, the
# median, the third quartile and the maximum
# Inputs: a list of numbers called numbers
# Outputs: minimum, q1, median, q3, maximum
def calculateStatistics(numbers):
print "In calculateStatistics(numbers)"
return 1, 2, 3, 4, 5
# printBoxPlot() takes the 5 statistical values,
# prints them and the box plot for them.
# Inputs: minimum, q1, median, q3, maximum
# Output: none
def printBoxPlot(minimum, q1, median, q3, maximum):
printBoxPlotGraph(minimum, q1, median, q3, maximum)
print "min:", minimum
print "Q1:", q1
print "median:", median
print "Q3:", q3
print "max:", maximum
# printBoxPlotGraph() takes the 5 statistical values
# and prints just the box plot graph for them.
# Inputs: minimum, q1, median, q3, maximum
# Output: none
def printBoxPlotGraph(minimum, q1, median, q3, maximum):
# find the sizes of the pieces
whiskerLeftSize = q1 - minimum
boxLeftSize = median - q1
boxRightSize = q3 - median
whiskerRightSize = maximum - q3
# construct the pieces
# the space before the minimum
blankLeft = ' ' * minimum
whiskerLeft = '-' * whiskerLeftSize
boxLeft = ' ' * boxLeftSize
boxRight = ' ' * boxRightSize
whiskerRight = '-' * whiskerRightSize
# concatenate the pieces
# break this into left & right so lines don't wrap
left = blankLeft + '|' + whiskerLeft + '[' + boxLeft + '|'
right = boxRight + ']' + whiskerRight + '|'
boxplot = left + right
print boxplot
def main():
printGreeting()
numberList = getInputFromUser()
minimum, q1, median, q3, maximum = calculateStatistics(numberList)
printBoxPlot(minimum, q1, median, q3, maximum)
printBoxPlotGraph(1, 3, 5, 8, 11)
# getInputFromUser() prompts the user for how he will
# give input, either from a file or from the terminal
# gets the input and returns it.
# Inputs: none
# Output: a list of numbers
def getInputFromUser():
choice = 'invalid'
while choice != 'file' and choice != 'type':
choice = raw_input("Where is the input? (type 'file' or 'type') ")
if choice == 'file':
return getInputFromFile()
elif choice == 'type':
return getInputFromTerminal()
# getInputFromFile() opens the file indicated by the
# user, reads the numerical data from it, closes the
# file and returns the list of numbers.
# Inputs: none
# Output: a list of numbers
def getInputFromFile():
print "In getInputFromFile()"
return []
# getInputFromTerminal() gets the numerical
# data from the keyboard as the user enters
# it and returns the list of numbers.
# Inputs: none
# Output: a list of numbers
def getInputFromTerminal():
print "In getInputFromTerminal()"
return []
# getInputFromTerminal() gets the numerical
# data from the keyboard as the user enters
# it and returns the list of numbers.
# Inputs: none
# Output: a list of numbers
def getInputFromTerminal():
n = int(input("How many numbers are there? "))
# initialize an empty list
numberList = []
for i in range(n):
newNumber = int(input('> '))
# add this new number to the end of the number list
numberList.append(newNumber)
# return the number list
return numberList
Where is the input? (type 'file' or 'type') type How many numbers are there? 4 > 9 > 3 > 5 > 1 test: [9, 3, 5, 1]
Success!
# calculateStatistics() takes a list of numbers and
# calculates the minimum, the first quartile, the
# median, the third quartile and the maximum
# Inputs: a list of numbers called numbers
# Outputs: minimum, q1, median, q3, maximum
def calculateStatistics(numbers):
# sort the numbers
# luckily something exists for this...
numbers.sort()
# len(mylist) returns the number of items in it
n = len(numbers)
# the minimum will be the first item in the list
minimum = numbers[0]
# the maximum will be the last item in the list
maximum = numbers[n - 1]
# the median will be the in the n/2 index
# notice the integer division!
median = numbers[n / 2]
# and the quartiles...
q1 = numbers[n / 4]
q3 = numbers[3 * n / 4]
# finally, return everything
return minimum, q1, median, q3, maximum
print "[min, q1, median, q3, max]" print calculateStatistics([1, 2, 3, 4, 5, 6, 7, 8, 9]) print calculateStatistics([9, 7, 5, 3, 1, 2, 4, 6, 8]) print calculateStatistics([5]) print calculateStatistics([1, 2])
[min, q1, median, q3, max] (1, 3, 5, 7, 9) (1, 3, 5, 7, 9) (5, 5, 5, 5, 5) (1, 1, 2, 2, 2)
Success!
# Filename: boxplot.py
# Author: Don Miner & Sue Evans
# Date: 8/22/09
# Section: All
# Email: bogar@cs.umbc.edu
#
# This program will produce a box plot for the
# numerical data the user provides either from
# a file or from typing at the terminal.
# printGreeting() prints an explanation of the program
# Inputs: none
# Output: none
def printGreeting():
print "\nThis program will produce a box plot"
print "for the numerical data you enter."
print "Welcome to my box plot program!\n"
# getInputFromUser() prompts the user for how he will
# give input, either from a file or from the terminal
# gets the input and returns it.
# Inputs: none
# Output: a list of numbers
def getInputFromUser():
choice = 'invalid'
while choice != 'file' and choice != 'type':
choice = raw_input("Where is the input? (type 'file' or 'type') ")
if choice == 'file':
return getInputFromFile()
elif choice == 'type':
return getInputFromTerminal()
# getInputFromFile() opens the file indicated by the
# user, reads the numerical data from it, closes the
# file and returns the list of numbers.
# Inputs: none
# Output: a list of numbers
def getInputFromFile():
print "In getInputFromFile()"
return []
# getInputFromTerminal() gets the numerical
# data from the keyboard as the user enters
# it and returns the list of numbers.
# Inputs: none
# Output: a list of numbers
def getInputFromTerminal():
n = int(input("How many numbers are there? "))
# initialize an empty list
numberList = []
for i in range(n):
newNumber = int(input('> '))
# add this new number to the end of the number list
numberList.append(newNumber)
# return the number list
return numberList
# calculateStatistics() takes a list of numbers and
# calculates the minimum, the first quartile, the
# median, the third quartile and the maximum
# Inputs: a list of numbers called numbers
# Outputs: minimum, q1, median, q3, maximum
def calculateStatistics(numbers):
# sort the numbers
# luckily something exists for this...
numbers.sort()
# len(mylist) returns the number of items in it
n = len(numbers)
# the minimum will be the first item in the list
minimum = numbers[0]
# the maximum will be the last item in the list
maximum = numbers[n - 1]
# the median will be the in the n/2 index
# notice the integer division!
median = numbers[n / 2]
# and the quartiles...
q1 = numbers[n / 4]
q3 = numbers[3 * n / 4]
# finally, return everything
return minimum, q1, median, q3, maximum
# printBoxPlot() takes the 5 statistical values,
# prints them and the box plot for them.
# Inputs: minimum, q1, median, q3, maximum
# Output: none
def printBoxPlot(minimum, q1, median, q3, maximum):
printBoxPlotGraph(minimum, q1, median, q3, maximum)
print "min:", minimum
print "Q1:", q1
print "median:", median
print "Q3:", q3
print "max:", maximum
# printBoxPlotGraph() takes the 5 statistical values
# and prints just the box plot graph for them.
# Inputs: minimum, q1, median, q3, maximum
# Output: none
def printBoxPlotGraph(minimum, q1, median, q3, maximum):
# find the sizes of the pieces
whiskerLeftSize = q1 - minimum
boxLeftSize = median - q1
boxRightSize = q3 - median
whiskerRightSize = maximum - q3
# construct the pieces
# the space before the minimum
blankLeft = ' ' * minimum
whiskerLeft = '-' * whiskerLeftSize
boxLeft = ' ' * boxLeftSize
boxRight = ' ' * boxRightSize
whiskerRight = '-' * whiskerRightSize
# concatenate the pieces
# break this into left & right so lines don't wrap
left = blankLeft + '|' + whiskerLeft + '[' + boxLeft + '|'
right = boxRight + ']' + whiskerRight + '|'
boxplot = left + right
print boxplot
def main():
printGreeting()
numberList = getInputFromUser()
minimum, q1, median, q3, maximum = calculateStatistics(numberList)
printBoxPlot(minimum, q1, median, q3, maximum)
main()
linuxserver1.cs.umbc.edu[111] python boxplot.py This program will produce a box plot for the numerical data you enter. Welcome to my box plot program! Where is the input? (type 'file' or 'type') type How many numbers are there? 9 > 1 > 2 > 3 > 4 > 5 > 6 > 7 > 8 > 9 |--[ | ]--| min: 1 Q1: 3 median: 5 Q3: 7 max: 9 linuxserver1.cs.umbc.edu[112]
2 17 2 12 16 8 18 12 18 8 14 11 17 18 13 4 14 13 12 11 10 6 6 7 19 13 9 17 9 1 17 2 11 9 8 6 11 12 17 17 19 3 14 5 19 9 17 7 11 15 8 9 16 6 17 2 6 11 8 16 3 11 14 9 3 10 13 6 10 3 2 10 8 15 11 19 5 13 6 7 6 7 2 13 1 10 13 9 15 15 17 15 3 13 4 18 14 17 8 19
# getInputFromFile() opens the file indicated by the
# user, reads the numerical data from it, closes the
# file and returns the list of numbers.
# Inputs: none
# Output: a list of numbers
def getInputFromFile():
# initialize an empty list
numberList = []
filename = raw_input("Enter the filename : ")
file = open(filename, "r")
for number in file:
newNumber = eval(number)
numberList.append(newNumber)
file.close()
return numberList
numList = getInputFromFile() print numList
linuxserver1.cs.umbc.edu[135] python boxplot.py Enter the filename : numbers.dat [2, 17, 2, 12, 16, 8, 18, 12, 18, 8, 14, 11, 17, 18, 13, 4, 14, 13, 12, 11, 10, 6, 6, 7, 19, 13, 9, 17, 9, 1, 17, 2, 11, 9, 8, 6, 11, 12, 17, 17, 19, 3, 14, 5, 19, 9, 17, 7, 11, 15, 8, 9, 16, 6, 17, 2, 6, 11, 8, 16, 3, 11, 14, 9, 3, 10, 13, 6, 10, 3, 2, 10, 8, 15, 11, 19, 5, 13, 6, 7, 6, 7, 2, 13, 1, 10, 13, 9, 15, 15, 17, 15, 3, 13, 4, 18, 14, 17, 8, 19] linuxserver1.cs.umbc.edu[136]
Success!
ite207-pc-01.cs.umbc.edu[136] python boxplot.py This program will produce a box plot for the numerical data you enter. Welcome to my box plot program! Where is the input? (type 'file' or 'type') type How many numbers are there? 9 > 1 > 2 > 3 > 4 > 5 > 6 > 7 > 8 > 9 |--[ | ]--| min: 1 Q1: 3 median: 5 Q3: 7 max: 9 ite207-pc-01.cs.umbc.edu[137] python boxplot.py This program will produce a box plot for the numerical data you enter. Welcome to my box plot program! Where is the input? (type 'file' or 'type') file Enter the filename : numbers.dat |------[ | ]----| min: 1 Q1: 7 median: 11 Q3: 15 max: 19 ite207-pc-01.cs.umbc.edu[138]
def main():
print "\nThis program will produce a box plot"
print "for the numerical data you enter."
print "Hello, welcome to my box plot program!\n"
choice = 'invalid'
while choice != 'file' and choice != 'type':
choice = raw_input("Where is the input? (type 'file' or 'type') ")
numbers = []
if choice == 'file':
filename = raw_input("Enter the filename : ")
file = open(filename, "r")
for number in file:
newNumber = eval(number)
numbers.append(newNumber)
file.close()
elif choice == 'type':
n = int(input("How many numbers are there? "))
for i in range(n):
newNumber = int(input('> '))
# add this new number to the end of the number list
numbers.append(newNumber)
# sort the numbers
# luckily something exists for this...
numbers.sort()
# len(mylist) returns the number of items in it
n = len(numbers)
# the minimum will be the first item in the list
minimum = numbers[0]
# the maximum will be the last item in the list
maximum = numbers[n - 1]
# the median will be the in the n/2 index
# notice the integer division!
median = numbers[n / 2]
# and the quartiles...
q1 = numbers[n / 4]
q3 = numbers[3 * n / 4]
# find the sizes of the pieces
whiskerLeftSize = q1 - minimum
boxLeftSize = median - q1
boxRightSize = q3 - median
whiskerRightSize = maximum - q3
# construct the pieces
# the space before the minimum
blankLeft = ' ' * minimum
whiskerLeft = '-' * whiskerLeftSize
boxLeft = ' ' * boxLeftSize
boxRight = ' ' * boxRightSize
whiskerRight = '-' * whiskerRightSize
# concatenate the pieces
left = blankLeft + '|' + whiskerLeft + '[' + boxLeft + '|'
right = boxRight + ']' + whiskerRight + '|'
boxplot = left + right
print boxplot
print "min:", minimum
print "Q1:", q1
print "median:", median
print "Q3:", q3
print "max:", maximum
Draw a design diagram for the following project:
Project description:
This project allows the user to compute the volume and surface area of boxes, when s/he inputs the length, width and height of a box. The user can continue to enter the dimensions of new boxes until s/he is done.
# Filename: rand1.py
# Author: Sue Evans
# Date: 10/20/09
# Section: All
# Email: bogar@cs.umbc.edu
#
# This program illustrates python automatically seeding
# the random number generator using the system's time,
# so the seed will be different everytime the program runs
# using random()
from random import random
for i in range(10):
for j in range(5):
number = random()
print "%.12f" % (number),
print
Here's the output from two runs:
linuxserver1.cs.umbc.edu[128] python rand1.py 0.943261480372 0.154005266066 0.844525974976 0.583765951220 0.238710918762 0.840630709372 0.792588202641 0.922412700010 0.406105887829 0.928238267395 0.368546449511 0.436283507343 0.134233342198 0.241690027160 0.549987196778 0.680875157308 0.891671479328 0.163688215656 0.356264886504 0.917510472125 0.536991538634 0.725870958470 0.061311983526 0.467390124198 0.841849165201 0.736892870516 0.616416745251 0.765799219193 0.688528381762 0.335759874218 0.713517554627 0.873412461417 0.946687666341 0.753602080884 0.797920356699 0.944693652515 0.065424134275 0.024200402342 0.708441209872 0.927037309789 0.455257650896 0.222231393534 0.920537903693 0.491643880902 0.244733255432 0.284381032317 0.524329119253 0.372705775886 0.079492870458 0.134190063063 linuxserver1.cs.umbc.edu[129] python rand1.py 0.822015872381 0.236398450478 0.496277031584 0.652754711980 0.430250909378 0.712871191620 0.456168190880 0.852566313990 0.643437647359 0.437319556849 0.193554550051 0.970620848238 0.008477434438 0.550374015106 0.429892280832 0.367912143435 0.263518888582 0.690646019624 0.301095452514 0.799951784722 0.553873714449 0.756633155350 0.044985173260 0.137729652020 0.880460160921 0.749262682891 0.620612164245 0.057671190146 0.494361182914 0.471051448670 0.217800777087 0.950471608505 0.086212696549 0.702363377091 0.310036957841 0.065677666387 0.661299499973 0.425212880176 0.499324519028 0.269682940655 0.366411218288 0.093996635968 0.180165188941 0.626948514247 0.688864919803 0.979156243757 0.905714196934 0.191048791602 0.601074564485 0.598188508617 linuxserver1.cs.umbc.edu[130]
# Filename: rand2.py
# Author: Sue Evans
# Date: 10/20/09
# Section: All
# Email: bogar@cs.umbc.edu
#
# This program illustrates python automatically seeding
# the random number generator using the system's time,
# so the seed will be different everytime the program runs
# using randrange() with a range of 1 to 1000, inclusive.
from random import randrange
for i in range(10):
for j in range(5):
number = randrange(1, 1001)
print "%7d" % (number),
print
Here's the output :
linuxserver1.cs.umbc.edu[133] python rand2.py
688 7 220 438 586
976 980 529 656 895
241 236 638 593 116
749 432 668 841 177
345 51 388 590 16
61 665 351 797 897
183 841 389 845 135
537 132 298 847 997
675 196 288 823 428
254 770 967 952 97
linuxserver1.cs.umbc.edu[134] python rand2.py
393 504 112 67 306
917 998 144 576 972
546 975 978 540 194
764 269 196 187 835
62 396 544 469 779
545 489 264 609 434
667 124 850 35 830
778 56 713 163 753
276 413 381 271 254
649 874 207 443 406
linuxserver1.cs.umbc.edu[135]
Write python code that will write 100 randomly-generated values between 1 and 19, inclusive, to a file called numbers.dat with one number per line.