<- previous index next ->
Myhill-Nerode theorem and minimization to eliminate useless states.
The Myhill-Nerode Theorem says the following three statements are equivalent:
1) The set L, a subset of Sigma star, is accepted by a DFA.
(We know this means L is a regular language.)
2) L is the union of some of the equivalence classes of a right
invariant(with respect to concatenation) equivalence relation
of finite index.
3) Let equivalence relation RL be defined by: xRLy if and only if
for all z in Sigma star, xz is in L exactly when yz is in L.
Then RL is of finite index.
The notation RL means an equivalence relation R over the language L.
The notation RM means an equivalence relation R over a machine M.
We know for every regular language L there is a machine M that
exactly accepts the strings in L.
Think of an equivalence relation as being true or false for a
specific pair of strings x and y. Thus xRy is true for some
set of pairs x and y. We will use a relation R such that
xRy <=> yRx x has a relation to y if and only if y has
the same relation to x. This is known as symmetric.
xRy and yRz implies xRz. This is known as transitive.
xRx is true. This is known as reflexive.
Our RL is defined xRLy <=> for all z in Sigma star (xz in L <=> yz in L)
Our RM is defined xRMy <=> xzRMyz for all z in Sigma star.
In other words delta(q0,xz) = delta(delta(q0,x),z)=
delta(delta(q0,y),z) = delta(q0,yz)
for x, y and z strings in Sigma star.
RM divides the set Sigma star into equivalence classes, one class for
each state reachable in M from the starting state q0. To get RL from
this we have to consider only the Final reachable states of M.
From this theorem comes the provable statement that there is a
smallest, fewest number of states, DFA for every regular language.
The labeling of the states is not important, thus the machines
are the same within an isomorphism. (iso=constant, morph=change)
Now for the algorithm that takes a DFA, we know how to reduce a NFA
or NFA-epsilon to a DFA, and produces a minimum state DFA.
-3) Start with a machine M = (Q, Sigma, delta, q0, F) as usual
-2) Remove from Q, F and delete all states that can not be reached from q0.
Remember a DFA is a directed graph with states as nodes. Thus use
a depth first search to mark all the reachable states. The unreachable
states, if any, are then eliminated and the algorithm proceeds.
-1) Build a two dimensional matrix labeling the right side q0, q1, ...
running down and denote this as the "p" first subscript.
Label the top as q0, q1, ... and denote this as the "q" second subscript
0) Put dashes in the major diagonal and the lower triangular part
of the matrix (everything below the diagonal). we will always use the
upper triangular part because xRMy = yRMx is symmetric. We will also
use (p,q) to index into the matrix with the subscript of the state
called "p" always less than the subscript of the state called "q".
We can have one of three things in a matrix location where there is
no dash. An X indicates a distinct state from our initialization
in step 1). A link indicates a list of matrix locations
(pi,qj), (pk,ql), ... that will get an x if this matrix location
ever gets an x. At the end, we will label all empty matrix locations
with a O. (Like tic-tac-toe) The "O" locations mean the p and q are
equivalent and will be the same state in the minimum machine.
(This is like {p,q} when we converted a NFA to a DFA. and is
the transitive closure just like in NFA to DFA.)
NOW FINALLY WE ARE READY for 1st Ed. Page 70, Figure 3.8 or
2nd Ed. Page 159.
1) For p in F and q in Q-F put an "X" in the matrix at (p,q)
This is the initialization step. Do not write over dashes.
These matrix locations will never change. An X or x at (p,q)
in the matrix means states p and q are distinct in the minimum
machine. If (p,q) has a dash, put the X in (q,p)
2) BIG LOOP TO END
For every pair of distinct states (p,q) in F X F do 3) through 7)
and for every pair of distinct states (p,q)
in (Q-F) x (Q-F) do 3) through 7)
(Actually we will always have the index of p < index of q and
p never equals q so we have fewer checks to make.)
3) 4) 5)
If for any input symbol 'a', (r,s) has an X or x then put an x at (p,q)
Check (s,r) if (r,s) has a dash. r=delta(p,a) and s=delta(q,a)
Also, if a list exists for (p,q) then mark all (pi,qj) in the list
with an x. Do it for (qj,pi) if (pi,qj) has a dash. You do not have
to write another x if one is there already.
6) 7)
If the (r,s) matrix location does not have an X or x, start a list
or add to the list (r,s). Of course, do not do this if r = s,
of if (r,s) is already on the list. Change (r,s) to (s,r) if
the subscript of the state r is larger than the subscript of the state s
END BIG LOOP
Now for an example, non trivial, where there is a reduction.
M = (Q, Sigma, delta, q0, F} and we have run a depth first search to
eliminate states from Q, F and delta that can not be reached from q0.
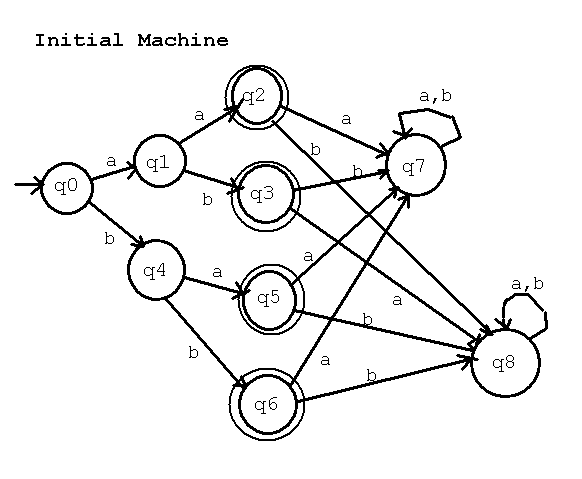
Q = {q0, q1, q2, q3, q4, q5, q6, q7, q8}
Sigma = {a, b}
q0 = q0
F = {q2, q3, q5, q6}
delta | a | b | note Q-F = {q0, q1, q4, q7, q8}
----+----+----+
q0 | q1 | q4 | We use an ordered F x F = {(q2, q3),
----+----+----+ (q2, q5),
q1 | q2 | q3 | (q2, q6),
----+----+----+ (q3, q5),
q2 | q7 | q8 | (q3, q6),
----+----+----+ (q5, q6)}
q3 | q8 | q7 |
----+----+----+ We use an ordered (Q-F) x (Q-F) = {(q0, q1),
q4 | q5 | q6 | (q0, q4),
----+----+----+ (q0, q7),
q5 | q7 | q8 | (q0, q8),
----+----+----+ (q1, q4),
q6 | q7 | q8 | (q1, q7),
----+----+----+ (q1, q8),
q7 | q7 | q7 | (q4, q7),
----+----+----+ (q4, q8),
q8 | q8 | q8 | (q7, q8)}
----+----+----+
Now, build the matrix labeling the "p" rows q0, q1, ...
and labeling the "q" columns q0, q1, ...
and put in dashes on the diagonal and below the diagonal
q0 q1 q2 q3 q4 q5 q6 q7 q8
+---+---+---+---+---+---+---+---+---+
q0 | - | | | | | | | | |
+---+---+---+---+---+---+---+---+---+
q1 | - | - | | | | | | | |
+---+---+---+---+---+---+---+---+---+
q2 | - | - | - | | | | | | |
+---+---+---+---+---+---+---+---+---+
q3 | - | - | - | - | | | | | |
+---+---+---+---+---+---+---+---+---+
q4 | - | - | - | - | - | | | | |
+---+---+---+---+---+---+---+---+---+
q5 | - | - | - | - | - | - | | | |
+---+---+---+---+---+---+---+---+---+
q6 | - | - | - | - | - | - | - | | |
+---+---+---+---+---+---+---+---+---+
q7 | - | - | - | - | - | - | - | - | |
+---+---+---+---+---+---+---+---+---+
q8 | - | - | - | - | - | - | - | - | - |
+---+---+---+---+---+---+---+---+---+
Now fill in for step 1) (p,q) such that p in F and q in (Q-F)
{ (q2, q0), (q2, q1), (q2, q4), (q2, q7), (q2, q8),
(q3, q0), (q3, q1), (q3, q4), (q3, q7), (q3, q8),
(q5, q0), (q5, q1), (q5, q4), (q5, q7), (q5, q8),
(q6, q0), (q6, q1), (q6, q4), (q6, q7), (q6, q8)}
q0 q1 q2 q3 q4 q5 q6 q7 q8
+---+---+---+---+---+---+---+---+---+
q0 | - | | X | X | | X | X | | |
+---+---+---+---+---+---+---+---+---+
q1 | - | - | X | X | | X | X | | |
+---+---+---+---+---+---+---+---+---+
q2 | - | - | - | | X | | | X | X |
+---+---+---+---+---+---+---+---+---+
q3 | - | - | - | - | X | | | X | X |
+---+---+---+---+---+---+---+---+---+
q4 | - | - | - | - | - | X | X | | |
+---+---+---+---+---+---+---+---+---+
q5 | - | - | - | - | - | - | | X | X |
+---+---+---+---+---+---+---+---+---+
q6 | - | - | - | - | - | - | - | X | X |
+---+---+---+---+---+---+---+---+---+
q7 | - | - | - | - | - | - | - | - | |
+---+---+---+---+---+---+---+---+---+
q8 | - | - | - | - | - | - | - | - | - |
+---+---+---+---+---+---+---+---+---+
Now fill in more x's by checking all the cases in step 2)
and apply steps 3) 4) 5) 6) and 7). Finish by filling in blank
matrix locations with "O".
For example (r,s) = (delta(p=q0,a), delta(q=q1,a)) so r=q1 and s= q2
Note that (q1,q2) has an X, thus (q0, q1) gets an "x"
Another from F x F (r,s) = (delta(p=q4,b), delta(q=q5,b)) so r=q6 and s=q8
thus since (q6, q8) has an X then (p,q) = (q4,q5) gets an "x"
It depends on the order of the choice of (p, q) in step 2) whether
a (p, q) gets added to a list in a cell or gets an "x".
Another (r,s) = (delta(p,a), delta(q,a)) where p=q0 and q=q8 then
s = delta(q0,a) = q1 and r = delta(q8,a) = q8 but (q1, q8) is blank.
Thus start a list in (q1, q8) and put (q0, q8) in this list.
[ This is what 7) says: put (p, q) on the list for (delta(p,a), delta(q,a))
and for our case the variable "a" happens to be the symbol "a".]
Eventually (q1, q8) will get an "x" and the list, including (q0, q8)
will get an "x'.
Performing the tedious task results in the matrix:
q0 q1 q2 q3 q4 q5 q6 q7 q8
+---+---+---+---+---+---+---+---+---+
q0 | - | x | X | X | x | X | X | x | x |
+---+---+---+---+---+---+---+---+---+
q1 | - | - | X | X | O | X | X | x | x | The "O" at (q1, q4) means {q1, q4}
+---+---+---+---+---+---+---+---+---+ is a state in the minimum machine
q2 | - | - | - | O | X | O | O | X | X |
+---+---+---+---+---+---+---+---+---+
q3 | - | - | - | - | X | O | O | X | X | The "O" for (q2, q3), (q2, q5) and
+---+---+---+---+---+---+---+---+---+ (q2, q6) means they are one state
q4 | - | - | - | - | - | X | X | x | x | {q2, q3, q5, q6} in the minimum
+---+---+---+---+---+---+---+---+---+ machine. many other "O" just
q5 | - | - | - | - | - | - | O | X | X | confirm this.
+---+---+---+---+---+---+---+---+---+
q6 | - | - | - | - | - | - | - | X | X |
+---+---+---+---+---+---+---+---+---+
q7 | - | - | - | - | - | - | - | - | O | The "O" in (q7, q8) means {q7, q8}
+---+---+---+---+---+---+---+---+---+ is one state in the minimum machine
q8 | - | - | - | - | - | - | - | - | - |
+---+---+---+---+---+---+---+---+---+
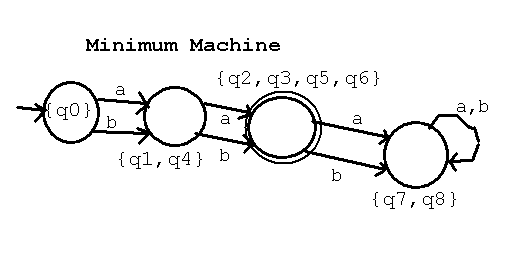
The resulting minimum machine is M' = (Q', Sigma, delta', q0', F')
with Q' = { {q0}, {q1,q4}, {q2,q3,q5,q6}, {q7,q8} } four states
F' = { {q2,q3,q5,q6} } only one final state
q0' = q0
delta' | a | b |
----------+----------------+------------------+
{q0} | {q1,q4} | {q1,q4} |
----------+----------------+------------------+
{q1,q4} | {q2,q3,q5,q6} | {q2,q3,q5,q6} |
----------+----------------+------------------+
{q2,q3,q5,q6} | {q7,q8} | {q7,q8} |
----------+----------------+------------------+
{q7,q8} | {q7,q8} | {q7,q8} |
----------+----------------+------------------+
Note: Fill in the first column of states first. Check that every
state occurs in some set and in only one set. Since this is a DFA
the next columns must use exactly the state names found in the
first column. e.g. q0 with input "a" goes to q1, but q1 is now {q1,q4}
Use the same technique as was used to convert a NFA to a DFA, but
in this case the result is always a DFA even though the states have
the strange looking names that appear to be sets, but are just
names of the states in the DFA.
It is possible for the entire matrix to be "X" or "x" at the end.
In this case the DFA started with the minimum number of states.
At the heart of the algorithm is the following:
The sets Q-F and F are disjoint, thus the pairs of states (Q-F) X (F)
are distinguishable, marked X. For the pairs of states (p,q) and (r,s)
where r=delta(p,a) and s=delta(q,a) if p is distinguishable from q,
then r is distinguishable from s, thus mark (r,s) with an x.
If you do not wish to do minimizations by hand,
on linux.gl.umbc.edu use
ln -s /afs/umbc.edu/users/s/q/squire/pub/myhill myhill
myhill < your.dfa # result is in myhill_temp.dfa
or get the C++ source code from
/afs/umbc.edu/users/s/q/squire/pub/download/myhill.cpp
Instructions to compile are comments in source code
instruction on use are here
<- previous index next ->

