CMSC 671

Artificial Intelligence -- Fall 2010

HOMEWORK TWO
out 9/22/10 due 10/13/10

As always, this assignment must be turned in as a hardcopy. You may either typeset your solution or handwrite them neatly.

PART I. Constraint Satisfaction (50 pts.)

In this question, you will be solving a map-coloring problem. In this domain, each of the regions on a map must be colored either black, gray, or red. The regions must be colored in such a way that no adjacent regions are the same color. Two regions are considered to be adjacent if they touch along an edge. (Two regions that touch only at a corner are not adjacent.) Here is the map that you'll be using for all of the questions in this section:

<MAP>

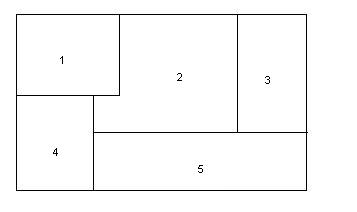
1. Backtracking search (15 pts)

Suppose you decide to use simple backtracking search to find a solution to this constraint satisfaction problem. The variable ordering heuristic you use is simply to instantiate the variables in numbered order. The value ordering heuristic is to consider the values in the order black, gray, red. You can use any reasonable shorthand to indicate the instantiations (e.g., "1=B" can mean region 1 is instantiated to the color black).

(a) Show the complete search tree, circling the solution node, if one is found.
(b) Show the final coloring, if one is found, on the map above or on a copy of the map.
(c) How many variable instantiations (search steps) are tried by this search method?

2. Forward checking (20 pts)

Now suppose we use forward checking to eliminate illegal values from the domains of uninstantiated variables. (Recall that in forward checking, only the constraints immediately connected to instantiated variables are checked.) Furthermore, suppose we use a variable ordering heuristic that chooses the variable with the fewest legal instantiations remaining to instantiate next. If more than one such variable exists, the one earlier in the numbered order is selected. The same value ordering heuristic is used as in backtracking search (i.e., consider first black, then gray, then red).

(a) Show the complete search tree for forward checking search. At each node, show the remaining legal values for the uninstantiated variables. For example, at the first node below the root, only region 1 will be colored, so you should indicate the legal values for variables 2, 3, 4, and 5. Continue until your search finds a solution or fails.
(b) Show the final coloring, if one is found, on a copy of the map above.
(c) How many variable instantiations are tried by this search method?

3. Solution spaces (15 pts)

(a) How large is the search space for this problem? That is, how many different colorings, legal or illegal, are there for the blank map shown above?
(b) For this map, how many different solutions (legal colorings) are there?

PART II. Game Playing (50 pts)

Recall the game of Nim that we played in class. Initially, there are k piles, each containing n_k sticks. Two players alternate turns, and at each turn the current player removes any positive number of sticks from one of the piles. At least one stick must be removed during a turn. The last player to remove a stick loses. We will represent a state in this game as a k+1-tuple:

[s₁ ... s_k p],

where si is in the interval [0,n_k], and represents the number of sticks remaining in pile i; and p is either A or B, representing which player's move is next.

For those problem, you will be considering Nim211, a variation of Nim with three piles: one containing two sticks and the others each containing one stick. Player A goes first, so the initial state is [211A].

1. Game Tree (15 points)

Draw the complete game tree for Nim32. The left-to-right order of actions taken should always be: remove 1 stick from pile 1, remove 2 sticks from pile 1, remove 1 stick from pile 2, remove 1 stick from pile 3. (Obviously you should only have branches for actions that are legal in a particular state.) We will ignore the issue of repeated states for this problem, so it's OK if a state appears in more than one place in your tree.

2. Minimax and Alpha-Beta (15 points)

(a) Mark the terminal nodes in the game tree you drew for Question II.1 with their utility values, using +1 to indicate a win for A (MAX), and -1 to indicate a win for B (MIN).
(b) Annotate each of the nodes in the tree with its backed-up minimax value.
(c) Circle the nodes that would be pruned by alpha-beta pruning using depth-first (left-to-right) search. (You should assume that the alpha values are initialized to -1, rather than -infinity, and that the beta values are initialized to +1, rather than +infinity.)

3. Expectiminimax (20 pts)

Now suppose that each player only gets to choose which pile to draw from, but not how many sticks to remove. Instead, the number of sticks removed is a random integer in the interval [0, s_k]. For example, if the player chooses pile 2 and there are two sticks remaining in pile 2, then with probability 1/3, no sticks are removed; with probability 1/3, one stick is removed; and with probabiity 1/3, two sticks are removed.

Draw the 2-ply expectiminimax tree (i.e., one move for each player). Use the expectiminimax tree to back up the expected, max, and min values at each node. For the static evaluation function, use the (backed-up) utility values from the game tree you generated in II.2.